夹逼法与圆周率
当我步行去上班或者晚上出门遛狗时,我苹果手机上的计步器会记录下我走过的距离。计算方法很简单:应用程序根据我的身高估算出我的步长,并计数我走的步数,然后将这两个数字相乘。那么,我走过的距离就等于步长乘以步数。
阿基米德在计算圆的周长和估算圆周率[1]时,利用的也是类似的思路。假设圆是一条路径,需要走很多步才能走完全程,如图2–1所示。

图2-1
每一步都用一条微小的直线来表示。用步数乘以每一步的长度,我们就可以估算出这条路径的长度。当然,这只是一个估计量,因为圆实际上并不是由直线组成的,而是由弯曲的弧组成的。当我们用直线来代替每一段弧时,就相当于走了点儿捷径。因此,近似值肯定小于圆形路径的实际长度。但至少在理论上,通过走足够多的步数,并且每一步的步长足够短,我们就可以尽可能精确地估算出圆形路径的长度。
阿基米德从由6条直线组成的路径开始,进行了一系列这样的计算。他之所以选择从六边形入手,是因为它是一个便利的“大本营”,适合作为这段艰难的计算之旅的起点。六边形的优点在于,阿基米德可以轻易地计算出它的周长,即绕六边形一周的总长度。图2–2中六边形的周长是圆的半径的6倍,为什么是6倍呢?因为六边形包含6个等边三角形,它们每条边的长度都等于圆的半径(图2–3)。
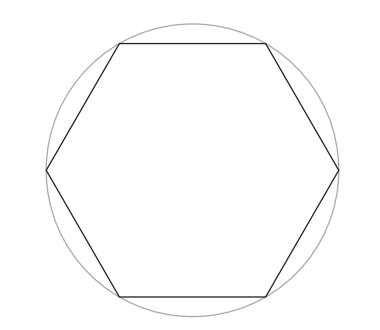
图2-2
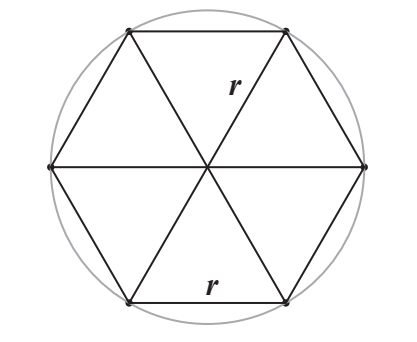
图2-3
其中,有6条三角形边构成了六边形的周长。
六边形的周长等于圆的半径的6倍,用符号可表示为p=6r。由于圆的周长C大于六边形的周长p,我们必定可以得出C>6r的结论。
这个论证给了阿基米德一个圆周率下限,圆周率用希腊字母π表示,其定义是圆的周长与直径之比。因为直径d=2r,不等式C>6r意味着:
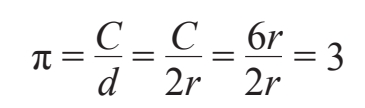
因此,该论证过程证明π>3。
当然,6是一个非常小的步数,六边形显然也不太像一个圆,但对阿基米德来说一切才刚开始。当从六边形中得出结论之后,他缩短了步长,并将步数翻倍。他的做法是,绕路到每段弧的中点处,用两小步取代之前的横跨弧的一大步(图2–4)。
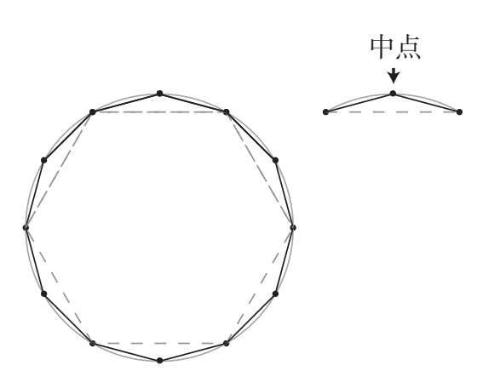
图2-4
之后,阿基米德不断重复这一做法。沉迷其中的他从6步到12步,然后是24步、48步、96步(图2–5),并以令人头痛不已的精密度算出了这些不断缩小的步长。
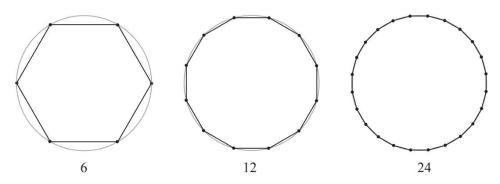
图2-5
遗憾的是,随着步长不断缩小,计算难度变得越来越大,因为他不得不借助勾股定理来确定步长。这就需要他用纸笔计算平方根,非常麻烦。此外,为了确保他算出的周长总是小于圆的周长,他必须保证当他需要近似分数被低估的时候,该值要取平方根的下限;而当他需要近似分数被高估的时候,该值则要取平方根的上限。
我想说的是,无论是在逻辑上还是在算术上,阿基米德计算π值的行为都堪称壮举。借助圆内接96边形和圆外接96边形,他最终证明π大于3+10/71而小于3+10/70。
让我们暂时忘掉数学,直观地欣赏一下这个结果:
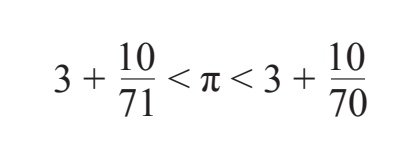
未知且永远不可知的π值被一个数值“虎钳”夹住了,挤在两个看起来几乎相同的数之间,它们唯一的区别在于,前一个数的分母是71,而后一个数的分母是70。不等式右边的3+10/70可以化简为22/7,它是今天所有学生仍在学习的那个著名的π的近似值,遗憾的是,也有些人误以为它就是π本身。
阿基米德使用的夹逼法建立在希腊数学家欧多克索斯的早期研究的基础之上,现在它被称作穷竭法,因为它将未知数π夹在两个已知数之间。随着步数不断加倍,界限将会越收越紧,π的取值范围也会越来越小。
圆是几何学中最简单的曲线。然而,令人惊讶的是,对圆的测量——用数字量化其属性——却超出了几何学的范畴。比如,欧几里得生活的年代比阿基米德早几十年,他的著作《几何原本》根本没有提到π。尽管你可以在这本书中找到运用穷竭法证明所有圆的面积与其半径平方之比都相等的证据,但它并未提到这个通用比率接近3.14。欧几里得的疏漏就是一个信号,表明我们还需要某种更深层次的东西。也就是说,求解π值需要一个新的数学分支,它能有效地处理曲线形状。如何测量曲线的长度、曲面的面积或者曲面体的体积,是让阿基米德深深着迷,并且引领他朝着积分学迈出第一步的前沿问题。求解出圆周率π的值,是积分学取得的第一次胜利。
[1] estimate pi: Stein, Archimedes, chapter 11, shows in detail how Archimedes did it.Be prepared for some hairy arithmetic.