积分学的圣杯
我想明确的一点是,基本定理不能完全解决面积问题。尽管它提供了关于面积变化率的信息,但我们仍要对面积本身进行推导。
用符号表示的话,基本定理告诉我们dA/dx=y,其中y(x)是已知函数。我们还需要找到能满足这个方程的A(x),等一下,这意味着我们突然又遇到了反向问题!事情发生了不同寻常的转变,我们本想解决第6章列出的第三个核心问题——面积问题,却遭遇了第二个核心问题——反向问题。我之所以称它为反向问题,是因为如图7–6所示,根据y推导出A意味着我们要沿箭头的反方向,去做函数求导的逆运算。在这种情况下,那个儿童游戏可能会变成:“我想的是一个面积函数A(x),它的导数是12x+x10–sinx,那么我想的面积函数是什么呢?”
于是,构建能解决12x+x10–sinx等任意曲线y(x)的反向问题的方法,就变成了微积分的圣杯。更准确地说,它是积分学的圣杯。一旦解决了反向问题,就可以彻底解决面积问题。换言之,已知任意曲线y(x),我们可以算出曲线下方的面积A(x);而通过解决反向问题,我们也可以解决面积问题。这就是我为什么说这两个问题是一出生即被分开的双胞胎,或者同一枚硬币的两面。
反向问题的解决方案还会产生更大的影响,原因如下:根据阿基米德的观点,面积是无穷多个无穷小的矩形条之和。因此,面积是一个积分,它是所有碎片重新拼凑起来的整体,是无穷小变化的累积。就像导数比斜率重要一样,积分也比面积重要。我们将在后面的章节中看到,面积对几何学而言至关重要,而积分对一切来说都至关重要。
处理棘手的反向问题的方法之一是无视它,把它搁在一边,并用更简单的正向问题(已知A,计算它的变化率dA/dx;根据基本定理,我们知道这个变化率一定等于我们正在寻找的y)取代它。相比反向问题,正向问题要容易得多,因为我们知道该从哪里着手去解决它。我们可以从已知的面积函数A(x)入手,然后运用标准导数公式计算它的变化率。由此得出的变化率dA/dx一定扮演着函数y的角色,因为基本定理向我们保证dA/dx=y。至此,我们就有了一对搭档函数A(x)和y(x),它们分别代表面积函数及其关联曲线。我们希望,如果有幸遇到需要我们计算特定曲线y(x)下方面积的问题,它对应的面积函数就是它的搭档A(x)。尽管这不是一种系统性方法,而且只在我们运气好的时候起作用,但它至少是一个容易的开端。为了增加成功的概率,我们的第一项任务是制作一张大查询表,以[A(x), y(x)]对的形式列出几百个面积函数及其关联曲线。那么,基于这张表的规模和多样性,我们找到解决真正的面积问题所需的搭档函数的概率将大幅增加。一旦找到那对必需的函数,我们就无须做进一步的工作了,因为答案就在那张表里。
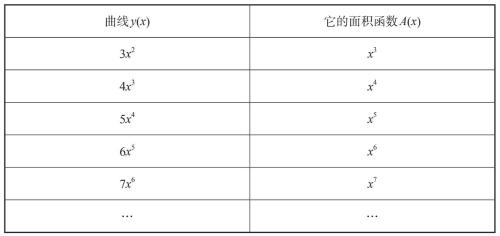
比如,在下一章我们将看到x3的导数是3x2,这个结果是我们通过解决正向问题,即进行简单的求导得出来的。然而,其中的奇妙之处在于,它告诉我们x3可以扮演A(x)的角色,而3x2可以扮演y(x)的角色。就这样,我们不费吹灰之力地解决了3x2的面积问题。以此类推,我们也可以将x的其他幂函数填到表中。如表7–1所示,x4的导数是4x3,x5的导数是5x4……一般而言,xn的导数是nxn–1。对幂函数来说,这些都是很容易得到的正向问题的答案。
表7-1
大学期间,22岁的牛顿在他的笔记本[1]里绘制过类似的表格,如图7–7所示。
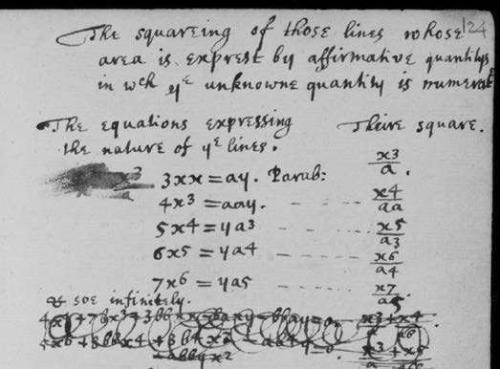
图7-7
请注意,牛顿的表述方式与我们有些许不同之处。上图中左边一列的曲线是“表达ye线性质的方程”,其面积函数是“它们的求积法”(因为他把面积问题视为“曲线的求积问题”)。为了确保所有量都具有恰当的维数,他觉得有必要插入任意长度单位a的不同次方,比如,从列表顶部向下数第5行,位于右下角的A(x)是x7/a5(而不是更简单的x7)。在牛顿看来,A(x)代表面积,因此对长度单位求积是必不可少的。所有这些内容都出现在“一种对那些可求积的曲线进行求积的方法”(宣告了微积分基本定理的诞生)之后的几页里,利用这个定理,牛顿花了更多页的篇幅列出了“曲线”及其“求积术”。在牛顿的操控下,微积分的机器运转起来了。
我们的第二项任务是,找到一种求任意曲线而不只是幂函数面积的方法。这其实是一种幻想,但它听起来太平常了,完全不像一个妙趣横生的幻想。不过,在我看来,这个问题包含了积分学之所以如此具有挑战性的精髓。如果曲线求积问题得到解决,它将引发连锁反应,就像被推倒的多米诺骨牌一样,一个接一个问题都会迎刃而解。而且,我们可以用它来回答笛卡儿眼中的那个超出人类理解范围的问题,即算出任意曲线的弧长。有了它,人们也有可能算出平面上任意一个不规则形状的面积,还可以计算球面、抛物面、瓮、桶及其他通过绕轴旋转曲线所得到的曲面(就像陶钧上的花瓶一样)的表面积、体积和重心。阿基米德和一位18世纪的数学天才思考过的关于曲线形状的经典问题,一下子就变得容易解决了。
不仅如此,某些预测问题也将得到解决。只要解决了曲线求积问题,我们就可以预测出运动物体在遥远未来的位置,比如,即使一颗行星受到的引力与我们宇宙中的引力不同,我们也能预测出某一时刻它在轨道上的位置。我之所以称曲线求积问题为积分学的圣杯,是因为许许多多的其他问题都可归结为这个问题,如果它被解决了,其他问题也会得到解决。
这就是算出任意曲线下方的面积如此重要的原因。由于面积问题与反向问题之间存在着密切的关系,所以它不只是与面积有关。面积问题也不只是关于形状,或者关于距离与速度之间的关系,或者关于其他狭义事物的问题,而是完全通用的。从现代的角度看,面积问题旨在预测以不断变化的速率变化的事物与它随时间的累积程度之间的关系。它与银行账户的波动性流入和累计余额有关;它与世界人口的增长率和地球上的净人口数有关;它与化疗药物在患者血液中不断变化的浓度和随时间的累积暴露剂量有关,因为总暴露量会影响化疗药物的效果和毒性。面积问题之所以重要,是因为未来对我们而言至关重要。
牛顿的新数学方法与不断变化的世界完美契合,因此,他把它命名为“流数术”(fluxion)。他谈到了流量(我们现在认为流量是时间的函数)及其流数(流量的导数或随时间的变化率),并明确了两个核心问题:
问题1:已知流量,如何求出它们的流数?(这相当于我们在前文中提到的正向问题,也就是求已知曲线的斜率,或者一般来说,求已知函数的变化率或导数的简单问题。这个过程在今天被称为微分。)
问题2:已知流数,如何求出它们的流量?(这相当于反向问题,也是面积问题的关键所在。它是根据斜率推导曲线,或者一般来说,根据变化率推导未知函数的困难问题。这个过程在今天被称为积分。)
问题2比问题1难得多,对预测和破解宇宙密码来说也更加重要。正式讨论牛顿在问题2上取得了怎样的成就之前,请允许我先阐明它为什么这么难。
[1] college notebook: You can explore Newton’s handwritten college notebook online.The page shown in the main text is http://cudl.lib.cam.ac.uk/view/MS-ADD-04000/260.