玩转幂级数

玩转幂级数

1664-1665年的冬天，牛顿在认真阅读沃利斯的《无穷算术》一书时，偶然发现了某个神奇的东西[1]。它是一种求解曲线下方面积的新方法，既简单又具有系统性。

实质上，沃利斯把无穷原则变成了一种算法。传统的无穷原则说的是，为了计算一个复杂的面积，人们可以把它重新想象成较简单面积的无穷级数。尽管牛顿遵循了这个策略，但他对其进行了升级，用符号而不是形状作为基本单元。他没有使用常见的碎片、条块或多边形，而是使用了符号x的次方，比如x2和x3。今天我们把他的策略称作幂级数法。

牛顿把幂级数视为无穷小数的一种自然推广形式。毕竟，一个无穷小数不过是10和1/10的幂级数。各个数位上的数字会告诉我们，它们分别包含多少个10或1/10的次方。比如，π=3.14…对应下面这个特定的组合：

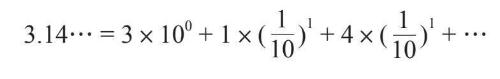
当然，根据无穷小数的要求，想以这种方式表示任何数，就需要使用无穷多个数字。通过类比，牛顿觉得他可以用无穷多个x的次方“配置”出任何曲线或函数。关键是要弄清楚其中包含多少个x的不同次方，在研究过程中，他想出了几种找到正确组合的方法。

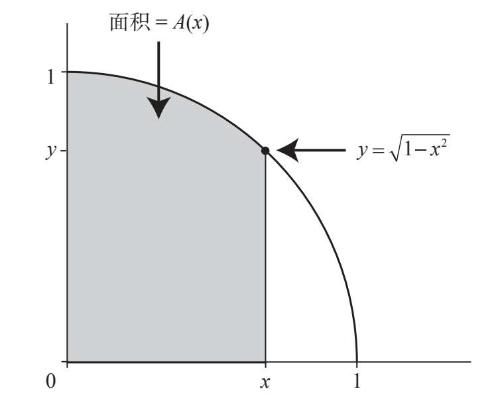
牛顿是在思考圆的面积问题时偶然想到了幂级数法。通过让这个古老的问题变得更具一般性，他在其中发现了一个前人未曾注意到的结构。他并没有把注意力局限在标准形状上，比如整圆或者1/4圆，而是专注于一种奇异的形状——“圆弓形”的面积，它的宽度为x，其中x是0到1之间的任意数字，1是圆的半径（图7–8）。

这是牛顿的第一个创举。使用变量x的好处在于，就像转动一个旋钮一样，他可以不断调整这个区域的形状。当x的值很小且接近于0时，就会产生一个细而竖直的圆弓形，看上去好像立在边缘处的细条；增大x会使这个圆弓形变宽为一个块状区域；当x的值为1时，则会得到他熟悉的形状——1/4圆。所以，通过上下转动旋钮，牛顿可以得到介于0和1之间的任意大小的x。

借助实验、模式识别和启发性猜测这个随心所欲的过程（他从沃利斯的书中学到的一种思考方式），牛顿发现圆弓形的面积可以用下面的幂级数来表示：

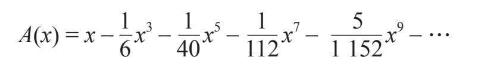
至于这些奇怪的分数来自哪里，或者算式中为什么只有x的奇数次方，这些都是牛顿的“独家秘方”。他构建这个幂级数的论证过程可以概括如下（如果你对他的论证过程不太感兴趣，可以跳过这一段的余下部分）：[2]牛顿在研究圆弓形之初，运用了解析几何的方法。他将圆表示为x2+y2=1，然后求解y，得到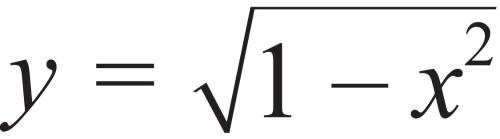。接着，他认为平方根等价于1/2次方，因此y=(1–x2)1/2，请注意括号右边的1/2次方。由于牛顿和其他人都不知道如何求解对应于1/2次方的圆弓形面积，所以他回避了这个问题（这是他的第二个创举），转而去求解对应于整数次方的圆弓形面积，后一个问题很容易解决，因为牛顿从沃利斯的书中习得了相关方法。于是，牛顿算出了y=(1–x2)1, (1–x2)2, (1–x2)3…（它们的括号外都是像1、2和3这样的整数）对应的圆弓形面积。他运用二项式定理将表达式展开后，发现它们都变成了简单幂函数的和，而这些幂函数正是我们在图7–7中看到的那些被他编制成表格的面积函数。之后，他开始寻找圆弓形面积随x变化的模式。根据对应于整数次方的圆弓形面积，牛顿猜出了对应于1/2次方的圆弓形面积（这是他的第三个创举），并用各种方法检验他的答案。这个答案引领他建立了A(x)的公式，也就是前文中展示的那个由奇异分数构成的令人惊叹的幂级数。

随后，圆弓形对应的幂级数的导数，引领他得到了圆对应的一个同样令人惊叹的级数：

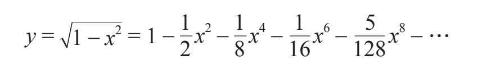
尽管他还会取得更多的研究成果，但到这一步已经相当了不起了。他用无穷多个更简单的部分构建出一个圆，这里的“更简单”是从积分和微分的角度说的。它的所有要素都是xn形式的幂函数，其中n是整数。而且，每个幂函数都有易于求解的导数和积分（面积函数）。同样地，xn的数值可以用简单的算数方法（重复的乘法运算）来计算，再用加、减、乘、除运算就可以把它们组合成一个级数。不需要取平方根，也无须担心会有其他难以处理的函数。如果牛顿能找到除圆之外的其他曲线对应的这类幂级数，那么它们的积分运算也会变得毫不费力。

就这样，年仅22岁的牛顿找到了通往圣杯的路径。通过将曲线转换成幂级数，他系统性地求解出它们的面积。考虑到他罗列在表格里的那些函数对，反向问题对幂函数来说简直是小菜一碟。因此，能用幂级数表示的任何曲线都是易于求解的。牛顿的算法可谓无比强大。

接着，他尝试了另一条曲线，即双曲线y=1/(1+x)，并且发现它也可以表示成幂级数的形式：

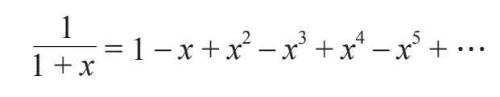
这个级数又让牛顿得出了双曲线下方从0到x的弓形（圆弓形的双曲线对应物）面积对应的幂级数。它定义的函数被他称为双曲线对数，我们今天称之为自然对数。

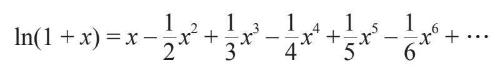
对数令牛顿兴奋不已的原因有两点。第一，它们可以极大地提高计算速度。第二，它们与牛顿当时正在研究的音乐理论中的一个争议性问题有关：如何在不牺牲传统音阶最令人愉悦的和声的前提下，将一个八度音程划分成完全相等的音步。（用音乐理论的术语来说，牛顿利用对数来评估八度音程的平均律划分与传统的纯律调音的效果有多么接近。）

得益于互联网创造的奇迹和“牛顿项目”历史学家的努力，你现在可以回到1665年，看看年轻的牛顿在做什么。（想免费翻看牛顿大学时期的笔记本，可以登录如下网址：http://cudl.lib.cam.ac.uk/view/MS ADD-04000/。）让我们越过他的肩膀看一下第223页（原稿第105页的背面），你会发现他正在比较音乐数列和几何数列。放大这一页的底部，你可以看到牛顿是如何把他的计算过程与对数联系起来的。然后翻到第43页（原稿第20页的正面），看看他如何“对双曲线求积”，以及利用幂级数计算1.1的自然对数值并将其精确到50位。

什么样的人能手工计算出50位的对数值呢？他似乎陶醉在幂级数赋予他的全新力量之中。当后来回忆起这种过度计算的行为时，他有点儿难为情地说：“我羞于告诉别人我算到了多少位，那时我没有其他事情可做，而且我实在太喜欢幂级数了。”[3]

唯一值得安慰的是，人无完人。当牛顿第一次做这样的计算时，他犯了一个小小的算术错误。他的计算结果中只有前28位数是正确的，但他后来发现并修正了这个错误。

在自然对数方面小试牛刀之后，牛顿又把他的幂级数延伸至三角函数，因为在天文学、测量学和航海中，每当出现圆、周期或三角形时，就会用到三角函数。不过，牛顿并不是第一个“吃螃蟹的人”。早在两个多世纪以前，印度喀拉拉邦的数学家[4]就发现了正弦、余弦和反正切函数的幂级数。16世纪早期，加斯特德维和尼拉坎撒·萨马亚吉在他们的著作中，将这些公式归功于喀拉拉邦数学与天文学院的创立者马德哈瓦。马德哈瓦推导出这些公式并以韵文的形式把它们表达出来，比牛顿早了大约250年。所以，我们说印度人应该预见到了幂级数的存在，这是有一定道理的。小数也发明于印度，而且正如我们看到的那样，牛顿认为他为曲线所做的一切就类似于无穷小数对算术的贡献。

这一切的关键在于，牛顿的幂级数给了他一把对付微积分的瑞士军刀。有了它们，他可以求积分、解代数方程的根和计算非代数函数（比如正弦、余弦和对数）的值。正如他所说，“在它们的帮助下，[5]几乎所有问题都得到了解决。”