行李箱的优化问题
费马微分学定理的雏形产生于他运用代数分析法解决优化问题[1]的过程中,优化问题研究的是如何以最佳方式做事情。根据具体情境,最佳可能意味着最快、最便宜、最大、最有利可图和最有效等。为了用最简单的方式阐明他的想法,费马设计了几个问题,它们听上去很像今天的数学老师给学生布置的练习题。所以,孩子们要怪就怪费马吧。
在根据我们的时代特点进行更新后,其中一个问题大致是:假设你想设计一个矩形的箱子来存放尽可能多的物品,但要满足两个约束条件。第一,这个箱子必须有一个正方形的横截面,宽x英寸[2],深x英寸。第二,它必须能放进某家航空公司的机舱行李架。根据航空公司对随身携带行李的规定,箱子的宽度、深度和高度之和不能超过45英寸。那么,当x是多少英寸时,箱子的容积最大呢?
解决这个问题的一种方法是运用常识。尝试几种可能性,比如,宽度和深度各为10英寸,那么高度可以是25英寸,因为10+10+25=45,这种尺寸的箱子的容积为10×10×25=2 500立方英寸[3]。立方体形状的箱子容积会不会更大呢?由于立方体的高度、宽度和深度必须相等,因此它的尺寸为15×15×15,容积是3 375立方英寸。在尝试了其他几种可能性之后,我们会发现立方体似乎是箱子形状的最佳选择。而且,事实的确如此。
所以,这本身并不是一个特别难解决的问题。我主要想用它来展示费马对于这类问题的推理方法,因为他的方法带来了更加了不起的成果。
和解决大多数代数问题一样,我们先要把所有给定的信息转化成符号。由于箱子的宽度和深度都是x,加起来就是2x。而且,箱子的高度、宽度和深度之和不能超过45英寸,所以它的高度是45–2x。那么,箱子的容积是x×x×(45–2x)=45x2–2x3,我们将其表示成V(x):
V(x)=45x2–2x3
如果我们以x为横轴、V(x)为纵轴,用计算机或绘图计算器画出图像,就会看到这条曲线先上升,并像预期的那样在x=15英寸时达到最大值,然后下降直至0(图4–3)。
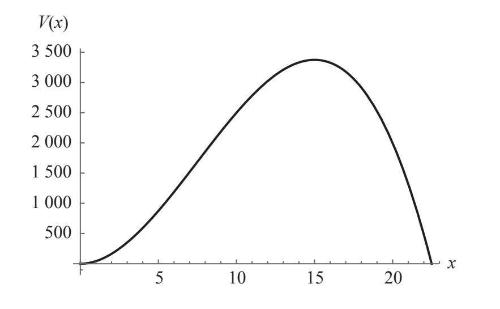
图4-3
我们也可以用学生们现在熟悉的微分学方法找出最大值,即求V(x)的导数并使其等于0。这种方法的思路是:曲线顶端的斜率为0,它在这里既不上升也不下降;由于斜率是用导数来衡量的,所以最大值处的导数必定为0。经过代数运算和对各种导数规则的运用,这个推理过程也会得出x=15的答案。
但是,费马没有绘图计算器或计算机,也没有导数的概念。那么,他是如何解决这个问题的呢?他利用了最大值的一个特性,即低于最大值的水平线都和曲线相交于两个点,如图4–4所示。
而高于最大值的水平线与曲线没有交点,如图4–5所示。
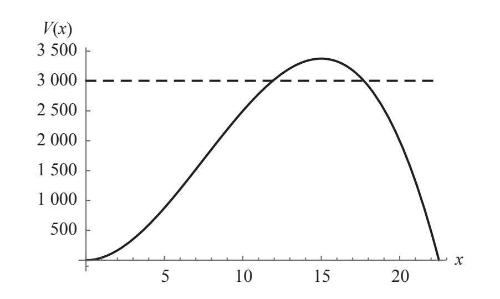
图4-4
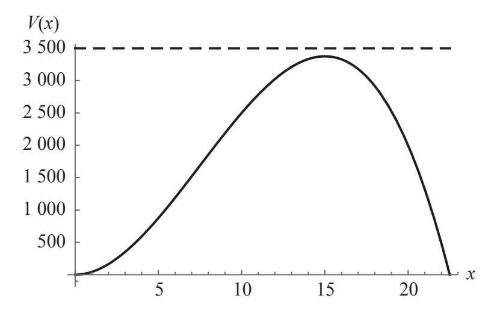
图4-5
这揭示了一种直观的解题策略。假设我们缓慢地抬升一条低于最大值的水平线,随着这条线逐渐上移,它的两个交点就像项链上的珠子一样沿着曲线向对方滑动(图4–6)。
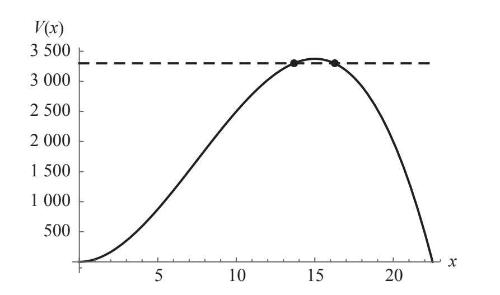
图4-6
在最大值处,这两个点发生碰撞。寻找碰撞点就是费马确定最大值的方法,换言之,他需要推导出两点合并为一点(形成“重交点”)的条件。有了正确的思路,余下的就是代数运算(符号处理)了。具体过程如下:
假设两个交点处的x分别为a和b,它们位于同一条水平线上,所以V(a)=V(b),即
45a2–2a3=45b2–2b3
为了做进一步运算,我们需要重新整理一下这个方程。如果我们把平方项放在一边,而把立方项放在另一边,可得:
45a2–45b2=2a3–2b3
运用高中代数的一些技巧,我们可以在方程两边进行因式分解,可得:
45(a–b)(a+b)=2(a–b)(a2+ab+b2)
然后,方程两边同时除以公因子(a–b),这是合乎规则的,因为a和b并不相等。[如果它们相等,方程两边同时除以(a–b)就相当于同时除以0,这是绝对不允许的。]消去(a–b)后得到的方程为:
45(a+b)=2(a2+ab+b2)
现在,请注意一个难以理解的逻辑点。费马先是假设a和b不相等,但他又假设当a和b在最大值处合并且相等时,他之前推导出的方程仍然成立。为了证明这样做是可行的,费马引入了一个被他称为“准等式”[4]的模糊概念。它是指在最大值处,a和b在某种程度上相等,但并不是真正相等(今天,我们用极限或者重交点的概念来表述它)。总之,他令a≈b,并大胆地用a替换上述方程中的b得到:
45(2a)=2(a2+a2+a2)
上式进一步化简为90a=6a2,它的解是a=0和a=15。第一个解a=0对应的是容积最小的箱子,它的宽度和深度都为0,体积也为0,我们对此毫无兴趣。第二个解a=15对应的是容积最大的箱子,它就是我们一直期待的答案,即15英寸是箱子的最佳宽度和深度。
从我们的角度看,费马的推理过程似乎有些奇怪,他不用导数就找到了最大值。今天,老师在讲优化问题之前会先教学生如何求导数,而费马的做法则完全相反。但这无关紧要,因为他和我们的想法是一样的。
[1] optimization problems: Mahoney, Mathematical Career, 199–201, dis cusses Fermat’s work on the maximization problem considered in the main text.
[2]1英寸=2.54厘米。——编者注
[3]1立方英寸≈16.39立方厘米。——编者注
[4] adequality: Ibid., 162–65, and Katz, History of Mathematics, 470–72.