关于切线的争论
费马的优化方法也使他明白了曲线的切线是怎么一回事,这是真正让笛卡儿火冒三丈的问题。
切线的英文单词“tangent”源于“touching”(触碰)的拉丁词根,这个术语用得很恰当,因为切线并不是从曲线中间穿过并与曲线交于两个点,而是在一个点上与曲线发生触碰,仅算得上擦肩而过(图4–15)。
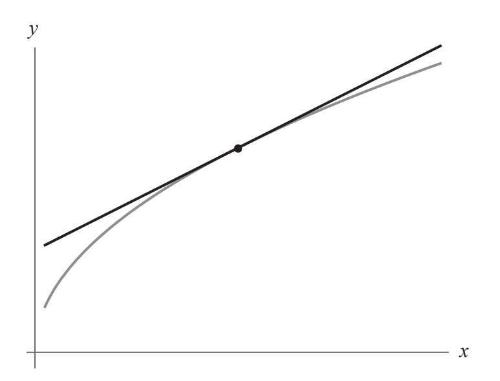
图4-15
确定切线的条件类似于求最大值或最小值的条件。如果我们让一条曲线与一条直线相交,然后不断地向上或向下滑动直线,当两个交点合而为一时,直线与曲线就相切了。
到17世纪20年代末的某个时候,费马已经找到了几乎所有代数曲线(只能用x和y的整数次幂来表示,而不含任何对数、正弦函数或其他超越函数的曲线)的切线。借助伟大的重交点概念,费马能用他的方法找出我们用求导法找到的所有切线。
笛卡儿有他自己的寻找切线的方法[1]。在1637年出版的《几何学》中,他自豪地向世人公布了他的方法。在不知道费马已经解决了这个问题的情况下,尽管笛卡儿也独立地想出了重交点的概念,但他用的是圆而不是直线去横穿曲线(图4–16)。在切点附近,一个标准的圆要么与曲线有两个交点,要么一个交点也没有。
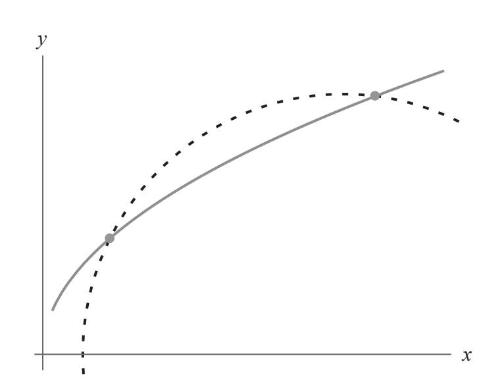
图4-16
通过调整圆的位置和半径,笛卡儿可以使两个交点合而为一。在那个重交点的位置上,圆与曲线恰好相切(图4–17)!
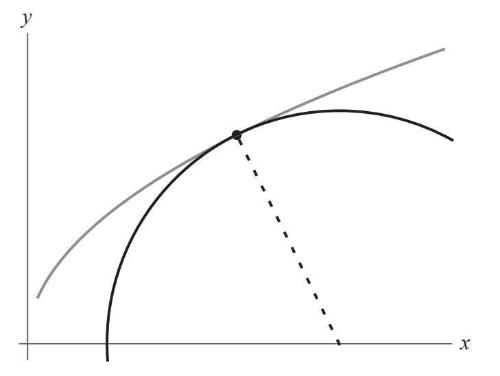
图4-17
这样一来,笛卡儿就得到了找出曲线切线所需的一切条件,他也找到了曲线的法线,它位于圆的半径方向上,与切线成直角。
笛卡儿的方法虽然正确却很笨拙,它涉及的代数运算量远超费马的方法。但是,笛卡儿尚未听说过费马,所以他以一贯的傲慢姿态自认为超越了所有人。他在《几何学》中得意扬扬地说:“关于如何在曲线上的任意一点处画出与其成直角的直线,我给出了一般性方法。[2]而且,我敢说这不仅是我所知道的几何学中最有用和最普遍的问题,也是我一直以来渴望了解的问题。”
1637年年末,当笛卡儿从巴黎的通信者那里得知,费马早在大约10年前就解决了切线问题但却一直未公之于众时,他感到很沮丧。1638年,他研究了费马的方法,试图寻找其中的漏洞。简直太多了!他通过一个中间人写信说:“我甚至不想提他的名字,[3]这样他就不会因为我发现的错误而感到十分羞耻。”笛卡儿对费马的逻辑提出了质疑,公平地说,费马的逻辑比较粗略,解释得也不详细。但最终,经过几次信件往来,费马从容地阐明了他的观点,笛卡儿也不得不承认费马的推理是有理有据的。
但在承认自己的失败之前,笛卡儿仍试图为难费马,要求他找出三次方程x3+y3=3axy的曲线切线,其中a是一个常数。笛卡儿知道用他自己的那种笨拙的方法无法找到这条切线(代数运算会变得无法处理),所以他相信费马也找不到。不过,费马是一个水平更高的数学家,方法也更好,他不费吹灰之力就画出了那条切线,令笛卡儿懊恼不已。
[1] Descartes had his own method: Katz, History of Mathematics, 472–73.
[2] “I have given a general method”: Quoted in Grattan-Guinness, From the Calculus, 16.
[3] “I do not even want to name him”: Quoted in Mahoney, Mathematical Career, 177.