通过微分推导出基本定理
莱布尼茨微分学的另一项成就在于,它让基本定理变得一目了然。回想一下,基本定理与面积累积函数A(x)有关,这个函数给出了曲线y=f(x)下方从0到x区间内的面积。基本定理认为,当我们向右滑动x时,曲线下方的面积会以f(x)的速率增大。因此,f(x)是A(x)的导数(图8–2)。
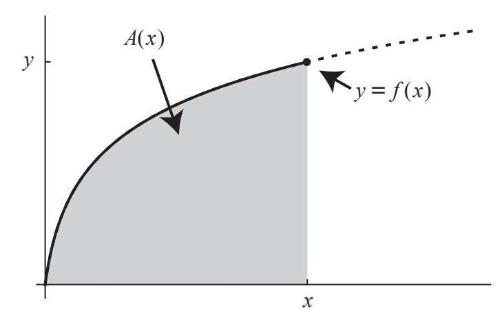
图8-2
为了弄清楚这个结果从何而来,假设我们给x增加一个无穷小量使它变为x+dx,那么面积A(x)会改变多少呢?根据定义,它的变化量应该是dA。因此,新的面积等于原来的面积加上面积的变化量,即A+dA。
一旦我们直观地展示出dA,基本定理就会立刻不证自明。如图8–3所示,无穷小的面积变化量dA是x和x+dx之间的无限细长的竖条面积。这个竖条是一个高为y、底为dx的矩形,所以它的面积等于高乘以底,即ydx,如果你喜欢,也可以写成f(x)dx。
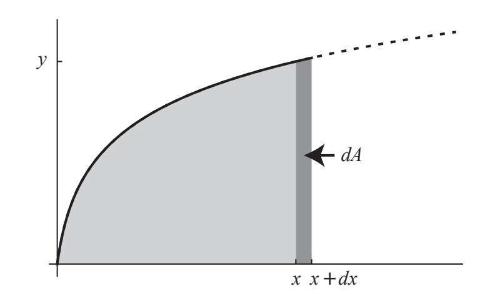
图8-3
实际上,只有在放大无穷倍的情况下,这个竖条才会是一个矩形。在现实中,对宽度为任意有限值Δx的竖条来说,面积的变化量ΔA由两个部分组成。占主导地位的部分是一个面积为yΔx的矩形,还有一个小得多的部分是矩形上方的类似三角形的微小的曲边“帽子”(图8–4)。
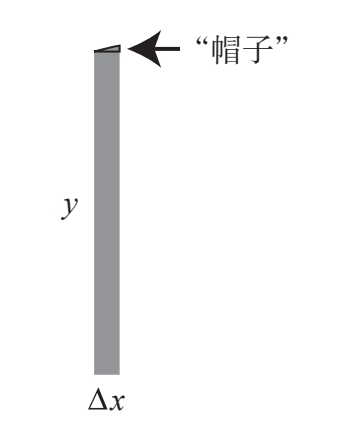
图8-4
这是另一个体现无穷小的世界比现实世界更美好的例子。在现实世界中,我们必须考虑这个“帽子”的面积,但它估算起来并不容易,因为它取决于“帽子”顶部曲线的具体情况。但当矩形的宽度趋于0并且“变成”dx时,相较于矩形的面积,“帽子”的面积就可以忽略不计。因为前者是小的部分,而后者是超小的部分。
所以,结果是:dA=ydx=f(x)dx。嘭!这就是微积分基本定理。或者,我们也可以把它写成今天更受欢迎的形式(在这个被误导的时代,微分已经被导数取代了):
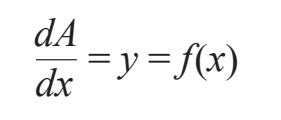
这正是我们在第7章利用油漆滚筒证明的结论。
还有最后一件事,当曲线下方的面积被视为无穷多个无穷小的矩形条的面积之和时,我们就可以把它写成:
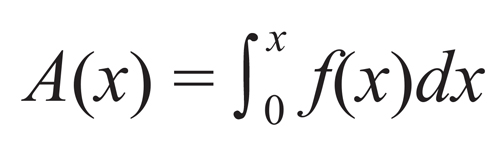
其中,那个像天鹅颈一样的符号实际上是一个拉伸的“S”,它提醒我们正在进行的是求和运算。它是积分学特有的一种求和运算,通过求无穷多个无穷小的矩形条面积之和,把它们整合成单一的连贯区域。这个表示整合的符号被称为积分号,莱布尼茨在1677年的一篇手稿中引入该符号,并在1686年进行了公开发表。积分号是微积分中最容易辨识的标志,它底部的0和顶部的x表示矩形在x轴上所处区间的端点,这些端点被称作积分限。