微分求导法

微分求导法

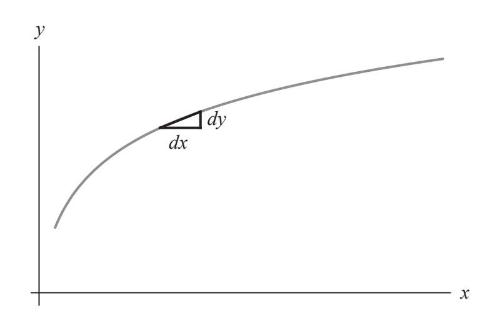
让我向你们展示一下，如果改用微分来表达，某些概念会变得多么简单。比如，当一条曲线被视为xy平面内的图像时，它的斜率是多少？我们从抛物线的相关研究（第6章）中了解到，曲线的斜率是y的导数，即当Δx趋于0时Δy/Δx的极限。但从微分的角度看，斜率又是什么呢？答案很简单：dy/dx，这就好像曲线是由很短的线段组成的一样（图8–1）。

如果我们把dy看作一个无穷小的垂直高度，把dx看作一个无穷小的水平距离，那么斜率一如既往地等于垂直高度除以水平距离，即dy/dx。

为了将其应用于一条特定的曲线（比如y=x3，也就是我们在计算略大于2的数的立方时思考过的例子），我们用以下方法计算dy：

y+dy=(x+dx)3

和前文中一样，我们将方程右边展开为：

(x+dx)3=x3+3x2dx+3x(dx)2+(dx)3

不过，按照秘诀，我们现在要舍弃(dx)2项和(dx)3项，因为它们并不是最大的部分。这样就有：

y+dy=(x+dx)3=x3+3x2dx

又因为y=x3，我们简化上面的方程得到：

dy=3x2dx

两边同时除以dx，得出相应的斜率：

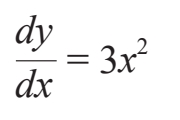
当x=2时，斜率为3×(2)2=12，跟我们在前文中看到的结果一样。这也是我们把2变为2.001后得到(2.001)3≈8.012的原因，它意味着，x相较于2的无穷小变化量（被称作dx）被转化为y相较于8的无穷小变化量（被称作dy），而且后者是前者的12倍（dy=12dx）。

顺便说一下，类似的推理过程表明，对于任意正整数n，y=xn的导数都是我们在前文中提过的dy/dx=nxn–1。稍做研究的话，我们就可以把这个结果推广至n为负数、小数和无理数的情况。

无穷小量和微分的巨大优势在于，它们提供了捷径，使计算变得更加简单。就像早些时候代数对几何学的影响一样，它们解放了人们的头脑，激发出更具创造性的想法。这也是莱布尼茨喜欢微分的原因，他在写给导师惠更斯的信中说，“我的微积分[1]几乎毫不犹豫地把目前关于这个学科的大部分发现都给了我。其中最令我欢喜的一点是，它在阿基米德几何方面赋予我们超越古人的优势，就像韦达和笛卡儿在欧几里得或阿波罗尼奥斯几何方面赋予我们的优势一样，使我们无须仅凭想象力去做研究。”

无穷小量唯一的缺陷在于，它们并不存在，至少在实数系中如此。哦，还有一件事：它们是自相矛盾的，即使真的存在，也没有任何意义。莱布尼茨的追随者之一约翰·伯努利意识到，尽管dx不为0，但无穷小量也必须满足像x+dx=x这样无意义的方程。好吧，你不可能拥有一切。一旦我们学会如何利用无穷小量，它们就会给出正确的答案。对我们而言，它们带来的好处可以大大弥补它们可能会造成的精神痛苦。就像毕加索眼中的艺术一样，它们也是能让我们了悟真相的“谎言”。

为了进一步证明无穷小量的力量，莱布尼茨又利用它们推导出斯涅尔的光折射正弦定律。第4章介绍过，当光从一种介质传播到另一种介质中（比如从空气进入水）时，它会发生弯折，其遵循的数学定律在几个世纪里被多次发现。尽管费马运用他的最短时间原理解释了这个问题，但他的核心目的其实是解决这个原理暗含的优化问题。莱布尼茨利用他的微分学轻松地推导出正弦定律，[2]并且自豪地指出：“其他学识渊博的人[3]大费周章得出的结论，精通微积分的人却好像拥有魔法一样只做了几步推导就搞定了。”