开普勒第二定律:相等的时间,相等的面积
开普勒从数据中发现了另一个定律。他的第一定律与行星的路径有关,而这个定律则与它们的速度有关。今天它被称为开普勒第二定律,说的是当行星沿轨道运行时,从这颗行星到太阳的假想连线在相等的时间内扫过的面积相等。
为了阐释这条定律的意思,假设我们能看到今晚火星在其椭圆轨道上的位置,并用一条直线把这一点与太阳连接起来(图3–7)。
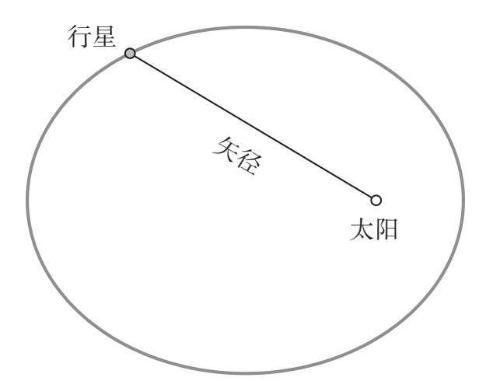
图3-7
现在,我们把这条线想象成一个类似于刮雨器的东西,太阳位于其枢轴点,火星则位于其顶端(只不过这个刮雨器不会像真正的刮雨器那样来回振动,它总是向前运动,而且速度非常缓慢)。当火星在接下来的几个晚上沿轨道前行时,刮雨器也随之移动,并在椭圆内部扫过一片区域。如果我们在一段时间(比如3个星期)再观察一次火星,就会发现缓慢移动的刮雨器已经扫出了一个扇形(图3–8)。
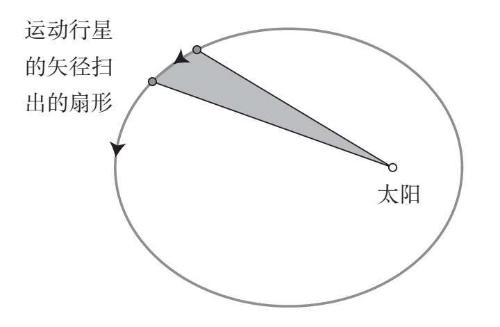
图3-8
开普勒发现,无论火星在其绕日轨道的哪个位置上,矢径在3个星期内扫过的扇形面积总是相等。而且,3个星期这个时间段也没有什么特别之处。如果我们在火星轨道上任意取两个时间间隔相等的点,不管它们在轨道的什么位置上,矢径扫过的扇形面积总是相等(图3–9)。
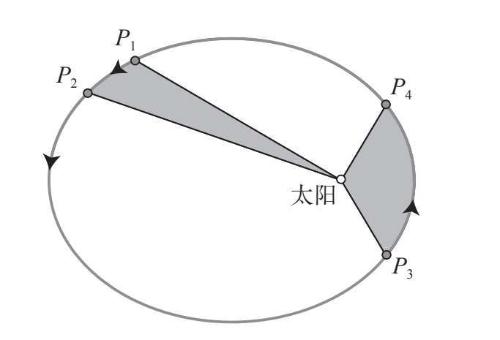
图3-9 如果时间(P1→P2)等于时间(P3→P4),那么两个扇形的面积相等
简言之,第二定律说明,行星并不以恒定的速度运行。相反,离太阳越近,它们的运行速度就越快。“在相等的时间内矢径扫过的面积相等”的陈述,可以使这个结论更加精确。
考虑到椭圆轨道内的扇形有一条弯曲的边,开普勒究竟是用什么方法测量出它的面积的?他采用了阿基米德的方法:先把扇形切割成许多小碎片,并把它们近似成三角形;然后算出这些三角形的面积(这很简单,因为它们的所有边都是直的),最后把结果加在一起,估算出原来的扇形面积。实际上,他利用了阿基米德版本的积分学,并将其应用于真实数据。