方程与曲线
可以肯定的是,费马和笛卡儿从未利用xy平面去研究像肉桂葡萄干面包这样的有形事物。对他们来说,xy平面是研究纯粹几何学的工具。
在他们各自的研究过程中,两个人都发现,任意一个线性方程(x和y只以一次幂形式出现的方程)在xy平面上都可以表示成一条直线。线性方程和直线之间的这种联系,会让人联想到有可能存在一种更深层次的联系,即非线性方程与曲线之间的联系。在像y=200x这样的线性方程中,变量x和y均独自出现,而没有平方、立方或者更高次方的形式。费马和笛卡儿意识到,他们可以构建他们想要的任何方程,对x和y进行他们想要的任何变换——将其中一个平方,将另一个立方,再将它们相乘或者相加——然后把结果诠释成一条曲线。幸运的话,它会是一条有趣的曲线,或许还是人们从未想象过或者阿基米德从未研究过的曲线。任何含有x和y的方程都是一次新的冒险,也是一种格式塔转换。你不是从一条曲线开始,而是从一个方程开始,看看它能描绘出什么样的曲线。这就好比让代数来驾车,而把几何学安置在后座上一样。
费马和笛卡儿从二次方程入手,在这类方程中,除了普通的常量(比如200)和线性项(比如x和y)之外,变量还可以平方或者相乘,产生像x2、y2和xy这样的二次项。传统上,平方量一直被解读为正方形区域的面积,因此,x2表示边长为x的正方形的面积。过去,人们认为面积是一个与长度或者体积完全不同的量;但对费马和笛卡儿来说,就像x、x3或者x的其他任意次方一样,x2只是另一个实数,这意味着它也可以被绘制在数轴上。
今天,学习高中代数的学生应该都能画出y=x2(对应的曲线是一条抛物线)之类方程的图像。值得注意的是,含有x和y的二次项但不含有它们的更高次方的其他所有方程,只对应着4类曲线,即抛物线、椭圆、双曲线或者圆(图4–2)。比如,二次方程xy=1的图像是双曲线,x2+y2=4的图像是圆,x2+2y2=4的图像是椭圆。即使像x2+2xy+y2+x+3y=2这样令人头疼的二次方程,也只对应着上述4类曲线中的一种,事实上它的图像是抛物线。
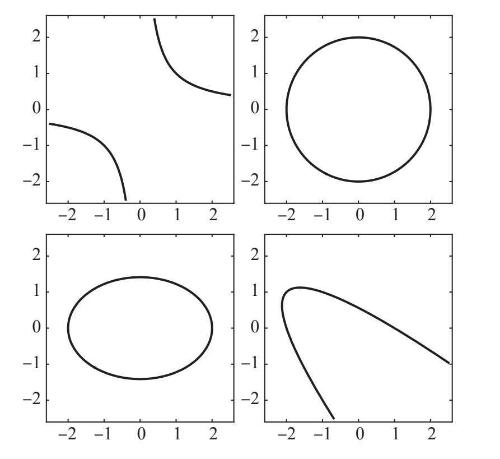
图4-2
费马和笛卡儿最先发现了这种奇妙的巧合:含有x和y的二次方程是希腊人研究的圆锥截面的代数对应物,这4类曲线是以不同角度切割圆锥体得到的。在费马和笛卡儿搭建的这个新舞台上,经典曲线像幽灵一样从迷雾中再次现身。