10的次方

10的次方

在科学领域，有很多我们用10的次方来简化计算的情况。特别是在数很大或很小的时候，用科学记数法来改写它们是一个好办法，即用10的次方尽可能简洁地表示这些数。

以21万亿为例，这是近来人们在谈论美国国债时常会提到的数字。21万亿可以用十进制记数法写成21 000 000 000 000，也可以用科学记数法写成21×1012=2.1×1013。如果出于某种原因，我们需要将这个很大的数乘以10亿，那么写成(2.1×1013)×109=2.1×1022会比用十进制记数法写出所有0要容易得多。

10的次方中的前三个是我们每天都会遇到的数：

1 101=10

2 102=100

3 103=1 000

请注意它们的变化趋势：左边一列(x)呈可加性增长，而右边一列(10x)呈可乘性增长，也就是我们预期的指数增长。因此，在左边一列中，每次都要在前一个数的基础上加1，而在右边一列中，每次都要在前一个数的基础上乘以10。加法和乘法之间这种有趣的对应关系，是指数函数（尤其是10的次方）具备的一个典型性特征。

根据这两列之间的对应关系，如果我们将左边一列中的两个数字相加，就相当于让它们在右边一列中的搭档相乘。比如，左边的1+2=3会转换为右边的10×100=1 000。这种从加法到乘法的转换是有意义的，原因是：

101+2=103=101×102

因此，当我们将10的次方相乘时，就可以让它们的指数像这里的1和2一样相加。一般性规则是：

10a×10b=10a+b

一个相关趋势是，左边一列中的减法对应于右边一列中的除法。

3–2=1对应于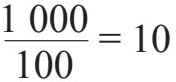

这些实用的模式表明，如何能让两列数字持续地变小。原则是，每当我们在左边一列中减去1，就应该让右边一列除以10。现在再看一下第一行：

1 101=10

2 102=100

3 103=1 000

由于左边一列减去1相当于右边一列除以10，因此这种对应关系在新的第一行（左边1–1=0，右边10/10=1）也成立。

0 100=1

1 101=10

2 102=100

3 103=1 000

这个推理过程解释了100为什么会被定义成1（并且只能这样定义），而它曾令许多人困惑不已。任何其他选择都会打破这种模式，这个定义是能延续左右两列数字的既定趋势的唯一选择。

同理，我们可以继续拓展这种对应关系。当左边一列是负数时，右边一列对应的数字就会变成分数，相当于1/10的次方：

-2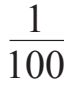

-1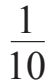

0 1

1 10

2 100

3 1 000

请注意，即使左边一列中的数字变成0或负数，右边一列中的数字也始终是正数。

在使用10的次方时，一个潜在的认知陷阱是，它们可以使截然不同的数看起来比实际情况更加相似。为了避免这个陷阱，我们可以假装10的不同次方形成了概念上的不同类别。有时为了做到这一点，人类语言会给10的不同次方指定不同的名字，就好像它们是毫不相关的“物种”一样。在英语中，我们用三个互不相关的词语来指代10、100和1 000，分别是：ten，a hundred和a thousand。这种做法很棒，因为它传递了一个正确的理念，那就是尽管这些数字都是10的相邻次方，但它们却有质的不同。任何了解5位数和6位数工资之间差别的人都知道，多一个0可是意义非凡。

当表示10的次方的词语听起来太过相像时，我们就会被引入歧途。在2016年美国总统大选期间，参议员伯尼·桑德斯频频谴责“百万富翁和亿万富翁”享受了过高的税收减免福利。遗憾的是，不管你是否认同他的政治观点，他的这句话听上去都会让人觉得，就财富而言，百万富翁和亿万富翁似乎可以相提并论。事实上，亿万富翁可比百万富翁富有得多。想要知道100万和10亿有多么不同，我们可以这样比较：100万秒还不到2个星期，而10亿秒大约是32年。前者只是一个假期的时间，而后者则是人生的重要组成部分。

这个例子给予我们的教训是，必须谨慎使用10的次方。它们是十分强大的压缩机，能把巨大的数字缩减到更易于我们理解的程度，这也是它们如此受科学家欢迎的原因。在某个量的变化涉及许多数量级的情况下，人们通常会用10的次方来定义一个适当的测量尺度，这样的例子包括酸碱性的pH标度、地震的里氏震级和响度的分贝标度。比如，如果溶液的pH值从7（中性，比如纯水）变为2（酸性，比如柠檬汁），氢离子浓度就会增加5个数量级，即105或10万倍。尽管氢离子浓度的确变化了10万倍，但pH值从7降到2的量度方法让这个过程看似只走了5小步，根本没发生多大的变化。