自然对数及其指数函数

自然对数及其指数函数

尽管底数10在它的全盛时期曾大展拳脚，但在现代微积分中却很少用到，因为10已经被另一个看似深奥但其实远比它自然的底数取代了。这个底数被称作e，尽管它是一个接近2.718的数（我稍后会解释它从何而来），但它的数值无关紧要。关于e的很重要的一点是，以它为底的指数函数的增长速率恰好等于这个函数本身。

我再说一遍。

ex的增长率就是ex本身。

当指数函数被表示成以e为底数的形式时，这个不可思议的性质就可以简化所有计算。其他底数则享受不到这种简单性，无论我们用的是导数、积分、微分方程还是其他微积分工具，以e为底数的指数函数总是最简洁、最优雅和最美丽的。

除了它在微积分中起到的简化作用之外，底数e还自然而然地出现在金融和银行业中。下面这个例子将揭示数字e来自哪里，以及它是如何定义的。

假设你把100美元存入一家银行，它承诺支付的100%的年利率令人难以置信却又无法拒绝。这意味着一年以后，你的100美元将变成200美元。现在重新开始考虑一种对你更加有利的方案：假设你可以说服这家银行每年分两次为你账户里的钱计息，随着你的存款增加，你就可以从利息中获得利息。按照这个方案，你可以多赚多少钱呢？由于你要求银行分两次计息，只有每6个月的利率减半为50%才算公平。因此，6个月后，你将拥有100×1.50=150美元。再过6个月，也就是年末，你的存款金额将再次增加50%，变成150×1.50=225美元。这比你按照原来的计息方案得到的200美元多，因为你从这一年的利息中又获得了利息。

下一个问题是，如果你能让银行越发频繁地为你账户里的钱计息（相应地，每个复利期内的利率都会降低），会怎么样呢？你会获得惊人的财富吗？很遗憾，并不能。按季度计息的话，年末你将拥有100×（1.25）4≈244.14美元，这比225美元多不了多少。如果以更快的频率计息，比如一年365天每天计算一次，那么年末你只能得到：

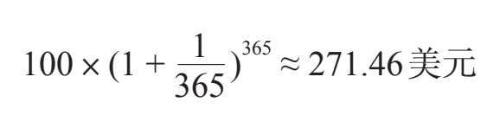
其中，分母和指数中的365指一年中的复利期数，1/365中的分子1指100%的利率。

最后，假设我们要让计息频率增加至极限。如果银行每年为你的钱计息n次，其中n是一个大得吓人的数字，相应地，在每个亚纳秒的复利期内利率也会变得极低。那么，与365个日复利期的结果相比，年末你的账户里会有：

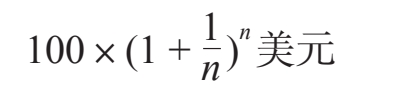
当n趋于无穷时，你的存款金额将趋于100与(1+1/n)n的乘积的极限，这个极限被定义为数字e。尽管我们并不清楚该极限值是多少，但事实证明它大约为2.718 28…。

在银行界，这种金融方案被称作连续复利。不过，我们的计算结果表明，它没那么令人兴奋。就上面的问题而言，年末你的账户余额是：

100×e≈271.83美元

尽管到目前为止这是最好的交易，但也只比每日计息多37美分。

我们刚刚花了很大的力气去定义e，结果证明它是一个复杂的极限。无穷是e的固有属性，就像数字π是圆的固有属性一样。你应该还记得，在确定π时需要计算一个圆内接正多边形的周长。当边数n趋于无穷而边长趋于0时，这个多边形就会趋近圆。数字e的定义方式在某种程度上与极限类似，只不过它是在连续复合增长这一不同的背景下产生的。

就像底数为10的指数函数写作10x一样，与e相关的指数函数写作xe。它乍看上去很怪异，但在结构层面上它和底数10是一样的，所有的原则和模式也都一样。比如，已知ex的值为90，想要求出x的话，我们可以像之前那样使用对数，只不过我们现在求解的是以e为底的对数，即自然对数，用lnx来表示。想要求出未知的x，使ex=90，我们可以打开科学计算器，先输入90，再按下lnx键，答案是：

ln 90≈4.449 8

想要检验它的话，就把这个数留在屏幕上，然后按下ex键，你应该会得到90这个答案。如前所述，对数和指数就像订书机和起钉器一样，可以撤销彼此的作用。

尽管这些内容听起来深奥难懂，而且常常难以察觉，但自然对数却非常实用。比如，它是投资者和银行家熟知的72法则的基础。想要估算在年回报率已知的情况下，你银行账户里的钱增加一倍所需的时间，就可以用72除以回报率。因此，如果年增长率为6%，那么你的钱将在12（72/6）年后增加一倍。这个经验法则遵从自然对数和指数增长的性质，如果利率足够低，就会行之有效。再比如，在古树或骨头的碳定年法和艺术鉴定争议的背后，自然对数也在发挥作用。在一个著名的案件中，几幅据称出自维米尔之手的画作最终被证明为赝品；[1]人们通过分析颜料中铅和镭的放射性同位素的衰变情况揭露了真相。这些例子表明，自然对数普遍存在于有指数增长和指数式衰减的领域。