微积分的三大核心问题

微积分的三大核心问题

为了给后面的讨论做好准备，从一开始我们的头脑中就必须有一幅大图景。如图6–1所示，微积分有三大核心问题：

1.正向问题：已知一条曲线，求它各处的斜率。

2.反向问题：已知一条曲线各处的斜率，求这条曲线。

3.面积问题：已知一条曲线，求曲线下方的面积。

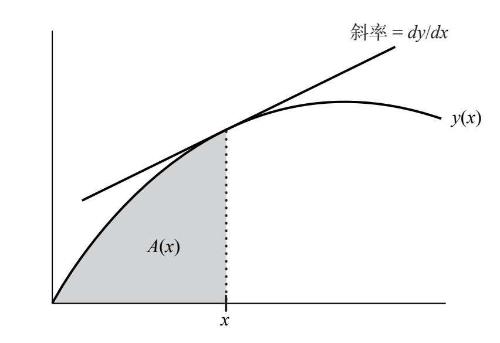
图6–1展示了泛型函数y(x)的图像，我没有说x和y代表什么，是因为这无关紧要。图中平面上的那条曲线能代表任意的一元函数，因此它可应用于涉及这类函数的任何数学或科学分支（基本上是所有地方）。至于它的斜率和面积的重要性，后文会做出解释。现在，我们把它们当作只有几何学家才会觉得伤脑筋的斜率和面积即可。

我们可以用两种方式来看待这条曲线，一种是老方式，一种是新方式。在17世纪早期微积分出现之前，这类曲线都被视为几何对象。它们本身就令人着迷，所以数学家试图量化它们的几何性质。已知一条曲线，他们想要算出曲线上每一点的切线斜率、曲线的弧长和曲线下方的面积，等等。到了21世纪，我们对产生曲线的函数更感兴趣，它能为通过曲线展示出来的某个自然现象或工艺流程建模。尽管曲线是数据，但支撑它的却是更深层次的东西。今天我们会把曲线看作沙滩上的脚印或者其形成过程的线索，我们更感兴趣的是函数建模的过程，而不是它留下的踪迹。

这两种观点之间的碰撞既是曲线之谜和运动之谜、变化之谜的碰撞，也是古代几何学与现代科学的碰撞。尽管我们身处现代，但由于对xy平面太熟悉了，所以我选择用更古老的视角去看待曲线问题。xy平面为我们理解微积分的三大核心问题提供了最清晰的方法，当我们用几何术语提出这3个问题时，它们马上就会变得直观起来。（在运动和变化方面，同样的理念也可以换种方式来表述，即用速度和距离等动态概念取代曲线和斜率。不过，要等到我们更好地掌握了几何学之后，才能这样做。）

这些问题应该从函数的角度去阐释。换句话说，当我谈到曲线的斜率时，我指的不是一个特定点的斜率，而是任意一点x的斜率。不同点的斜率不同，我们的目标就是了解斜率作为x的函数是如何变化的。同样地，曲线下方的面积也取决于x。在图6–1中我用灰色阴影来表示它，并将其标记为A(x)。这个面积也应该被看作x的函数，当x增加时，垂直的虚线向右滑动，面积随之扩大。

以上就是微积分的三大核心问题。那么，如何算出曲线的不断变化的斜率呢？如何根据斜率重建曲线呢？如何算出曲线下方不断变化的面积呢？

在几何学背景下，这些问题听起来可能相当枯燥无味。然而，一旦我们用21世纪的视角去看待运动问题和变化问题，在现实世界中重新诠释它们，它们的影响就会变得非常广泛和深远。斜率衡量的是变化率，而面积衡量的是变化的累积量。如前所述，斜率和面积会出现在物理学、工程学、金融学、医学等长期关注变化的所有领域。理解这些问题及其解决方法，可以开启现代定量思维（至少是关于一元函数）的世界。为了让大家有一个充分的了解，我应当指出微积分的相关内容还有很多，比如多元函数和微分方程等。等到适当的时候，我们再对这些内容进行讨论。

本章主要介绍一元函数及其导数（变化率），从以恒定速率变化的函数讲起，再转换到以不断变化的速率变化的复杂函数。理解不断变化的变化，才是微积分真正的闪光之处。

在习惯了变化率之后，我们就可以着手处理变化的累积量问题，这个更具挑战性的课题将放在下一章探讨。到那时我们会发现，尽管正向问题和反向问题看起来不一样，但它们是一出生就被分开的双胞胎，这个令人震惊的事实被称为微积分基本定理。它揭示了变化率和变化的累积量之间的关系比所有人认为的更密切，这一发现使微积分的两个部分成为有机的统一体。

不过，我们要先从变化率说起。