线性函数及其恒定的变化率
日常生活中的许多情形都是用线性关系——一个变量与另一个变量成正比——来描述的,比如:
1.去年夏天,我的大女儿莉亚在商场的一间服装店找到了她人生中的第一份工作。她的薪水是10美元/小时,工作2小时后她可以赚到20美元。一般而言,工作t小时后她可以赚到y美元,即y=10t。
2.一辆汽车以60英里/小时的速度行驶在公路上。那么,1小时后它行驶了60英里,2小时后它行驶了120英里,t小时后它行驶了60t英里。这里的关系式是y=60t,其中y是汽车在t小时后行驶的英里数。
3.根据《美国残疾人法案》,无障碍轮椅坡道每12英寸的水平距离对应的垂直高度不得超过1英寸。对一个达到最大允许坡度的坡道来说,垂直高度与水平距离之间的关系式是y=x/12,其中y是垂直高度,x是水平距离(图6–2)。
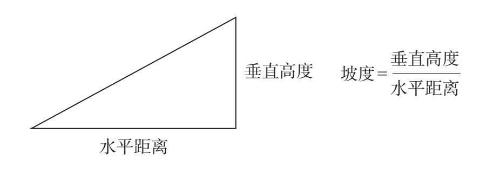
图6-2
在上述的每一种线性关系中,因变量相对于自变量的变化率都是恒定的。我女儿的报酬率是恒定的10美元/小时;汽车的速度是恒定的60英里/小时;无障碍轮椅坡道的坡度被定义为其垂直高度与水平距离之比,等于恒定的1/12。我喜欢吃的肉桂葡萄干面包也是这样,它提供热量的速率是恒定的200卡路里/片。
在微积分的专业术语中,变化率指两个变化量的商,也就是y的变化量除以x的变化量,写作Δy/Δx。如果我再吃掉两片面包,就又摄入了400卡路里的热量,对应的变化率是:
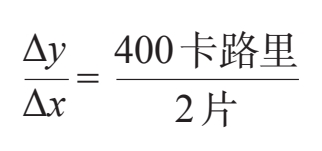
它可以化简为200卡路里/片。这没什么好惊讶的,但有趣的是,我们观察到这个变化率是恒定的。也就是说,不管我吃掉多少片面包,变化率都一样(图6–3)。
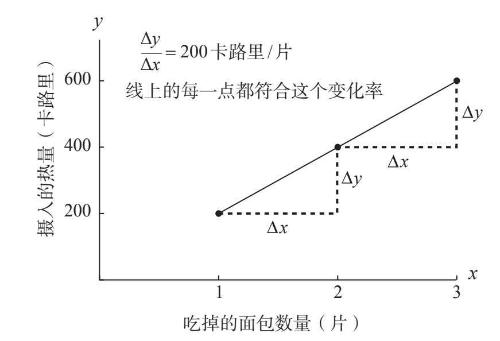
图6-3
当变化率恒定时,我们很容易把它们简单地看成是一个数字,比如200卡路里/片、10美元/小时或者1/12的坡度。尽管目前这不会造成什么问题,但之后却会让我们陷入麻烦。在更复杂的情况下,变化率并不是恒定的。假设我们行走在一段高低起伏的路上,有些路段陡峭,而有些路段平坦。对这段路来说,坡度是位置的函数,但把坡度仅看作一个数字就大错特错了。同样地,当汽车加速或者行星绕太阳旋转时,它们的速度也在不断变化。在这种情况下,把速度看作时间的函数显得至关重要。所以,我们现在应该养成一种习惯:不再把变化率看作数字,而将其视为函数。
这种概念混淆之所以会发生,是因为对我们一直在思考的线性关系来说,变化率函数是恒定的。这就是为什么在线性关系中把变化率当作数字是没有坏处的,它们不会随着自变量的变化而改变。我的女儿不管工作多长时间,她的报酬率都是10美元/小时,无障碍轮椅坡道上任意一处的坡度也都是1/12。但是,千万别被这些变化率蒙蔽了,它们仍然是函数,只不过碰巧是常函数。常函数的图像是一条平行于坐标轴的直线,如图6–4所示,肉桂葡萄干面包的有效负载是恒定的,为200卡路里/片。
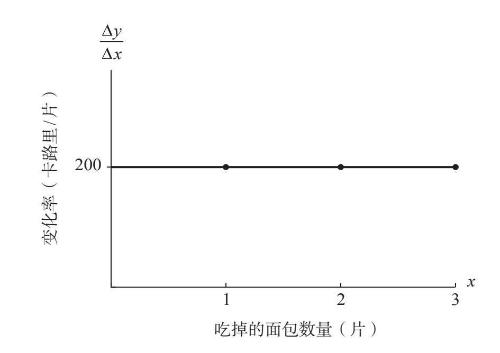
图6-4
在下一节讨论非线性关系的时候,我们会看到它在xy平面上生成的图像是一条曲线而非直线。不管怎样,直线或曲线总能显示出很多关于变量之间关系的信息,它们就像照片或签名一样,是揭示图像形成原因的重要线索。
请注意函数与函数图像之间的区别。函数是一种无实体的规则,代入x,得到y,而且每个x分别对应一个y。从这个意义上说,函数是无形的。当你看一个函数的时候,是什么也看不到的。它是一个幽灵般的存在,是一种抽象的规则。比如,这种规则可能是“给我输入一个数字,我将输出一个10倍于它的数字”。相比之下,函数图像是一种可见的、有形的事物,是一个你能看见的形状。具体来说,我刚才描述的函数图像是由方程y=10x定义的一条直线,它经过原点且斜率为10。但是,这个函数本身并不是直线,而是产生直线的规则。为了展示这个函数,你需要代入一个x,让它得出一个y,然后对所有x重复这一操作并将结果绘制成图像。你在这样做的时候,函数本身依然是不可见的,你看到的只是它的图像。