非线性函数及其不断变化的变化率
如果一个函数是非线性的,它的变化率Δy/Δx就不是常数。用几何术语来说,这意味着函数图像是一条各点斜率均不相同的曲线。我们以图6–5中的抛物线为例。
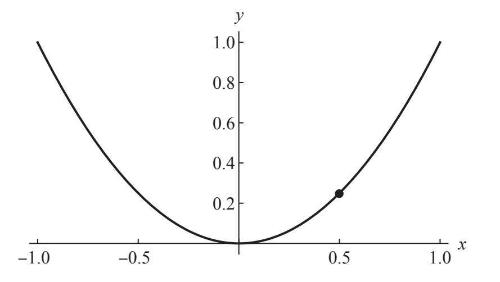
图6-5
图中是曲线y=x2,它对应于计算器上最简单的非线性按键——平方函数x2。这个例子将告诉我们导数作为切线斜率的定义的一些实际应用,也将阐明这个定义中为什么要用到极限。
检视这条抛物线,我们看到它的有些部分陡峭,而有些部分相对平坦。其中最平坦的部分出现在抛物线底部,即x=0的那一点。无须做计算我们就能看出来,这个点的导数必定是0。它也只能是0,因为底部的切线显然是x轴。如果把这条切线看作一个斜坡,它自始至终都没有上升,因此它的斜率为0。
但在抛物线的其他点上,切线斜率并不那么显而易见,事实上根本不明显。为了解决这个问题,我们做一个爱因斯坦式的思想实验。假设我们可以像扩洗照片那样放大抛物线上的任意一点(x, y),并让这个点始终处于视野的中心,那么我们会看到什么呢?就像我们在显微镜下观察曲线中的一段,并且逐渐增加放大率一样。随着镜头越来越近,这段抛物线看起来会越来越直。在放大无穷倍的极限情况下(相当于放大了我们感兴趣的那一点周围的一段无穷小的曲线),被放大的那一段曲线应该接近于一条直线。如果是这样,这条极限直线就会被定义为曲线上那一点的切线,它的斜率也会被定义为那一点的导数。
请注意,我们在这里利用的是无穷原则,即通过把一条复杂的曲线切分成无穷小的线段来简化它。在微积分领域,这是我们一直在做的事情。曲线形状很难对付,而直线形状即使无穷小且有无穷多个,处理起来也会容易得多。利用这种方法计算导数是微积分的一种典型操作,也是无穷原则最基本的应用之一。
为了进行思想实验,我们需要在曲线上选择一个点并放大它。尽管任意一点都可以,但为了数值上的便利,我们选择的是抛物线上x=1/2对应的那个点。在图6–5中,我用一个小圆点将它标示出来。在xy平面上,这个点位于(x, y)=(1/2, 1/4),或者可以用十进制表示为(x, y)=(0.5, 0.25)。在该点上y等于1/4的原因在于,为了成为这条抛物线上的一个点,它必须像抛物线上的所有点那样遵从y=x2。毕竟,这是判定一个点是否在这条抛物线上的标准。因此,当x=1/2时,这个点的y值必须为:
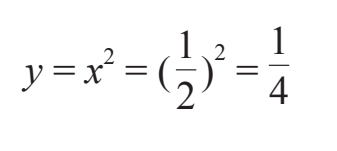
现在,我们准备放大这个点。先把点(x, y)=(0.5, 0.25)放置于显微镜的视野中心,再借助计算机图形学放大该点附近的一小段曲线,第一次放大的结果如图6–6所示。
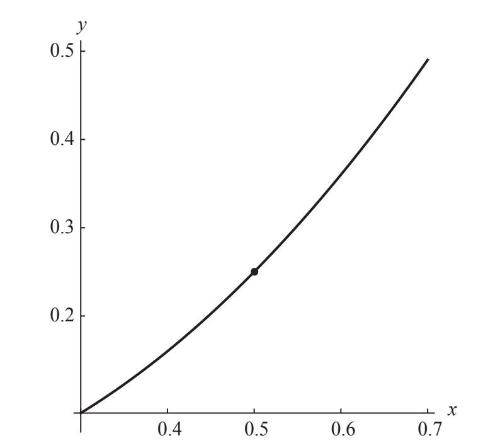
图6-6
抛物线的整体形状在这个放大的视图中消失了,相反,我们只能看到一段略微弯曲的弧。这一小段抛物线位于x=0.3和x=0.7之间,它的弯曲程度看起来要比整条抛物线小很多。
我们进一步放大x=0.49和x=0.51之间的那段抛物线,如图6–7所示。尽管这幅新的放大图像看起来比上一幅更直,但它并不是真正的直线,而仍为抛物线的一部分。
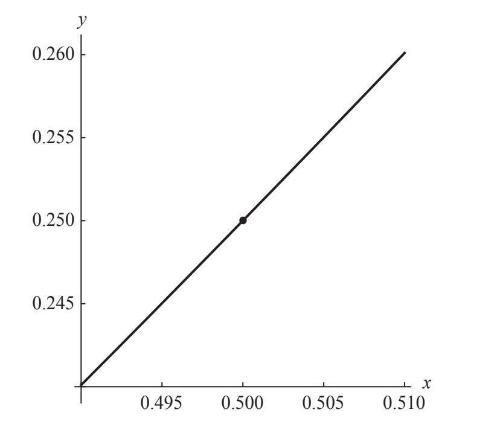
图6-7
其中的趋势显而易见。随着我们继续放大图像,视野中的那段抛物线看起来越来越直。对这个几乎变成直线的部分来说,我们计算它的垂直高度与水平距离之比Δy/Δx,实际上就是在求解当Δx趋于0时这段抛物线斜率(Δy/Δx)的极限值。计算机图形学有力地表明,这个部分的斜率越来越接近1,相当于一条45度角的直线。
借助一点儿代数知识,我们可以证明这里的极限斜率就是1(在第8章,我们将会看到具体的计算过程)。此外,不仅是在x=1/2处,在x取任意值时执行相同的计算,都可以得出抛物线上任意一点(x, y)的极限斜率或切线斜率等于2x。用微积分术语来说,x2的导数是2x。
尽管在继续讨论之前我很想证明一下这个求导法则,但让我们先接受它,看看它是什么意思。首先,它说在x=1/2处,斜率应该是2x=2×(1/2)=1,这正是我们在图像中看到的。其次,它预测在抛物线底部(x=0处)斜率应该是2×0=0,我们已经看到这也是正确的。最后,2x这个公式意味着,当我们向右延伸抛物线时斜率应该会增加。因为当x变大时,斜率(2x)也应该变大,抛物线应该变得更陡峭,而且事实的确如此。
这个抛物线实验有助于我们理解关于导数的一些注意事项。只有当被放大的曲线逼近极限直线时,我们才能定义导数。而对某些病态曲线来说,情况就不一样了。比如,如果有一条曲线呈V形,即在某个点上有一个尖角,那么当我们放大这个点时,它看起来仍然像一个角。无论放大多少倍,这个角都不会消失,曲线看上去也永远不会像直线。因此,V形曲线在拐角处没有明确的切线或斜率,在这一点上也就没有导数。
然而,如果一条曲线在任何一点处被充分放大之后,它看起来越来越直,我们就说这条曲线是光滑的。在本书中,我一直像先驱那样,假设微积分的曲线和过程都是光滑的。但在现代微积分领域,我们已经学会了如何处理非光滑曲线。在实际应用中,由于物理系统的突跳或其他不连续性行为,非光滑曲线的不便性和反常性时常会凸显出来。比如,当我们打开电路中的一个开关时,电流就会从完全不流动变为突然大幅度地流动。随着电流的接通,电流–时间图像会显示出一个几乎垂直的突然上升趋势,近似于不连续跳跃。有时我们将这种突然转变当作真正的不连续跳跃会更省事,在这种情况下,作为时间函数的电流在开关被打开的瞬间是没有导数的。
在高中或大学期间,微积分的第一堂课大多讲的都是求导法则,比如,x2的导数是2x,sinx的导数是cosx,lnx的导数是1/x,等等。然而,考虑到我们的目的,理解导数的概念并了解如何将它的抽象定义应用于实践,这些才是更重要的事。因此,让我们把目光投向现实世界。