作为昼长变化率的导数
在第4章,我们分析了昼长随季节变化的数据。当时我们的目的是阐明正弦波、曲线拟合和数据压缩的概念,而现在我们的目的是利用这些数据解释多变的变化率,并将导数引入另一个情境。
之前的数据涉及纽约市2018年每一天的白昼分钟数(从日出到日落的时长)。在这个背景下,相关的导数就是昼长从这一天到下一天的加长或缩短速率。比如,1月1日,从日出到日落的时间是9小时19分23秒;1月2日,昼长加长了一点儿,为9小时20分5秒。1月2日比1月1日多出来的42秒(相当于0.7分钟)就是衡量一年中这一天的昼长变化率的指标,即昼长正在以大约0.7分钟/天的速率加长。
为了进行比较,我们看看两周后(1月15日)的昼长变化率。从这一天到下一天,昼长增加了90秒,相当于以1.5分钟/天的速率在加长,是两周前测量的昼长变化率(0.7分钟/天)的两倍多。因此,昼长不仅在1月份不断加长,而且加长速率越来越快。
这种令人愉快的趋势将持续几个星期。随着春天的到来,昼长越来越长,加长速率也越来越快。在3月20日春分这一天,加长速率达到峰值,每天的加长量是前所未有的2.72分钟。你可以在第4章的图4–7中找到这一天,它是2018年的第79天,离左侧大约有1/4的距离,从中可以看出昼长波形图在这里的上升幅度最大。不难理解,图像最陡峭的地方就是加长速率最快的地方,这意味着此处的导数最大,而且昼长在尽可能快地加长。所有这些都发生在春季的第一天。
为了进行足够鲜明的对比,想想一年中昼长最短的那些日子,它们可谓是祸不单行。在冬天那些阴沉沉的日子里,昼长不仅短得令人沮丧,每天也没有太大的变化,只是越发地死气沉沉。不过,这也可以理解。昼长最短的日子出现在昼长波形图的底部,那里的波形是平坦的(否则它就不是底部,而会上升或下降),即导数为0,这意味着它的变化率会慢慢地变成0(至少是暂时的)。在那样的日子里,人们感觉春天似乎永远也不会到来了。
尽管我强调了一年之中对许多人来说具有情感意义的两个时间,即春分和冬至前后,但把一年的昼长情况当作一个整体来考虑会更具启发性。为了跟踪昼长变化率随季节的变化趋势,我从1月1日开始,每两个星期计算一次昼长变化率,直至12月31日,结果如图6–8所示。
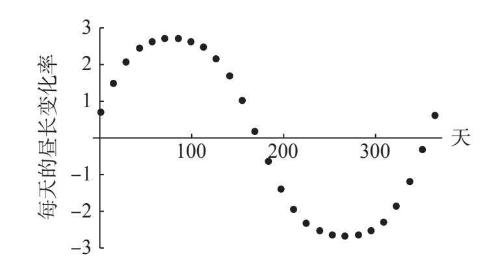
图6-8
纵轴表示每天的昼长变化率,即从这一天到下一天增加的白昼分钟数。横轴表示哪一天,用从1(1月1日)到365(12月31日)的数字来表示。
昼长变化率像波浪一样上下起伏。它一开始在冬末和初春是正值,那时昼长正在加长,并在第79天(3月20日,春分)前后达到峰值。我们已经知道,那是昼长变化率最快的时候,大约为每天加长2.72分钟。但此后昼长变化率开始下降,并在第172天(6月21日,夏至)之后变为负值。这是因为昼长从那时开始缩短,也就是下一天的昼长会比这一天短。昼长变化率在9月22日前后触底,此时昼长缩短得最快,之后一直到第355天(12月21日,冬至)昼长变化率都是负值(但缩短速率越来越慢),此后昼长会在不知不觉中再次加长。
把这个波形图与第4章的波形图放在一起比较,是一件非常有意思的事。当把它们绘制在一个图表中并重新调整至振幅具有可比性后,就会得到图6–9。(为了强调波的重复性,我在这里展示了两年的数据。而且,为了强化它们之间的对比,我把所有点都连接起来,并移除了纵轴上的数字,以便将大家的注意力集中在波的形状和时间上。)
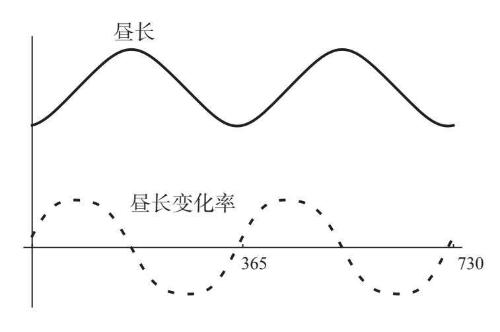
图6-9
我们要注意的第一件事是,这两个波是不同步的,它们不会同时达到峰值。表示昼长的波会在年中前后达到峰值,而表示昼长变化率的波会比前者早3个月达到峰值。这相当于提前了1/4个周期,因为每个波完成一次起伏运动需要花12个月的时间。
我们要注意的第二件事是,这两个波彼此相似,但又略有不同。尽管它们展现出明显的亲缘关系,但虚线波的对称性不如实线波,它的波峰和波谷也更平坦。
我之所以做上述分析,是因为这些现实世界中的波能让我们瞥见正弦波的一个不同寻常的性质:如果一个变量遵循完美的正弦波模式,那么它的变化率也是一个完美的正弦波,并且在时间上提前了1/4个周期。这种自我再生性质是正弦波特有的,而其他类型的波并不具备,它甚至可以当作正弦波的定义。从这个意义上说,我们的数据暗示了完美正弦波固有的神奇再生现象(等介绍傅里叶分析时我们会详细地介绍这一点,傅里叶分析是微积分的一个强大分支,今天它已经催生出微积分的一些十分振奋人心的应用。)
关于那1/4个周期的位移源自何处,接下来我会试着给你一些启发。同样的概念也可以解释为什么正弦波的变化率还是正弦波。关键在于,正弦波与匀速圆周运动有关。你应该还记得,当一个点以恒定的速度做圆周运动时,随着时间的流逝,它的垂直运动是一个正弦波(就此而言,它的水平运动也是一个正弦波)。带着这样的想法,我们来看图6–10。
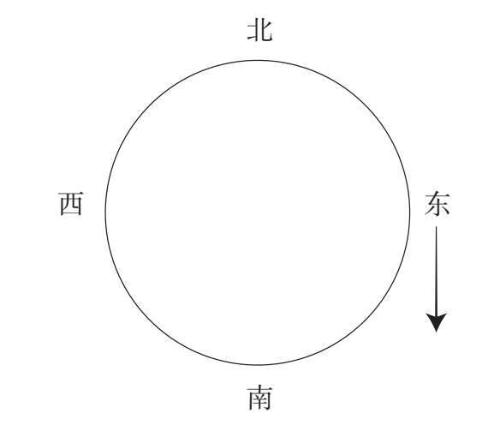
图6-10
上图展示了一个点正在绕圆周做顺时针运动,这个点不代表任何物理学或天文学对象。它既不是绕着太阳转的地球,与季节也没有任何关系,而只是一个做圆周运动的抽象点。它向东的位移会像正弦波一样增加和减少,当这个点向东的位移达到最大值时,它就类似于正弦波的峰值或者一年中昼长最长的一天。于是,问题出现了:当这个点在最东边,并且正弦波处于其向东位移的峰值时,接下来会发生什么?如图中箭头所示,最东边那一点是朝南的。南在罗盘上与东成90度角,而90度正好是一个周期的1/4。啊哈!这就是那1/4个周期的位移的来源。由于圆的几何结构,任何正弦波及其导数(变化率)的波之间总有1/4个周期的位移。在这个类比中,点的移动方向就像它的变化率,决定了这个点下一步的走向和位置。而且,在这个点做圆周运动的同时,箭头本身的罗航向也在以环形方式匀速旋转,因此它随时间发生的变化遵循正弦波模式。既然罗航向类似于变化率,那么变化率也遵循正弦波模式。这就是我们试图理解的自我再生性质,即正弦波会产生有90度位移的正弦波。(专业人士将会意识到我正在尝试抛开公式,去解释正弦函数的导数为什么是余弦函数,而余弦函数本身就是位移了1/4个周期的正弦函数。)
类似的90度相位滞后现象也出现在其他振动系统中。对一个来回摆动的钟摆而言,当通过底部时它的速度达到最大值,而它的摆角却要在1/4个周期之后,也就是在钟摆摆动到最右边时才会达到最大值。摆角–时间图像和速度–时间图像表明,它们是两个相似的正弦波,振动相位差为90度。
另一个例子是生物学领域的捕食者–被捕食者相互作用模型的简化版。假设有一群鲨鱼在捕食一群鱼,当这群鱼处于种群数量的最大值时,鲨鱼数量的增长速率最快,因为有很多鱼可以吃。鲨鱼数量会继续增加,并在1/4个周期后达到最大值,而此时鱼的数量已经开始下降,因为在1/4个周期之前,它们遭到了大肆捕食。对这个模型的分析表明,两个种群的振动相位差为90度。在自然界的其他地方也存在着类似的捕食者–被捕食者振动现象,比如,19世纪皮货贸易公司记录的加拿大野兔和山猫种群的每年波动情况(就像生物学领域中经常出现的情况一样,这些振动现象的真正原因无疑更加复杂)。
再次回到昼长数据,我们会看到它们并不是完美的正弦波。事实上,它们是一组离散的点,每天只有一个,两点之间也不存在其他数据。因此,它们不能提供微积分坚决要求的那种连续的点。在最后一个关于导数的例子中,我们要研究一种能以尽可能高的分辨率(精确至毫秒)来收集数据的情况。