运动使基本定理更直观
通过思考运动物体(比如跑步者或者汽车)行进的距离,我们可以直观地理解微积分基本定理:它讲了些什么,它为什么是正确的,以及它为什么很重要。基本定理不只是一个求解面积的技巧,也是预测我们关心之事的未来(在可能的情况下),以及解开宇宙中的运动和变化之谜的关键。
当牛顿动态地看待面积问题时,他发现了基本定理。他的想法是在这幅图景中引入时间和运动,用他的话说就是让面积流动起来,并不断扩大。
体现他这种想法的最简单例子是一辆以恒定速度行驶的汽车,其中距离等于速度乘以时间。尽管这个例子可能很简单,但它仍然抓住了基本定理的本质,算是一个不错的起点。
假设有一辆汽车以60英里/小时的速度沿公路行驶,我们分别绘制出它的距离–时间图像和速度–时间图像,如图7–1所示。
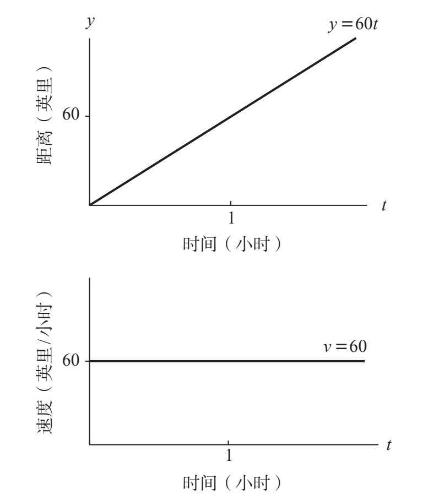
图7-1
我们先来看距离–时间图像(图7–1上图)。1小时后汽车行驶了60英里,2小时后汽车行驶了120英里,以此类推。总的来说,距离与时间的关系式为y=60t,其中y表示汽车在t小时后行驶的距离。我把y(t)=60t称为距离函数,它的图像是一条斜率为60英里/小时的直线。在我们还不知道速度的情况下,这个斜率可以告诉我们汽车的瞬时速度。在难度较大的问题中,速度可能会波动,不过在这里它是一个简单的常函数,即不管t是多少,都有v(t)=60,它的图像是一条平线(图7–1下图)。
我们已经看到速度在距离图像上是如何呈现的(作为直线的斜率),现在我们把这个问题反过来:距离在速度图像上是如何呈现的?换句话说,速度图像是否具有某种视觉或几何特征,能让我们推断出汽车在t小时后行驶的距离呢?当然有,汽车行驶的距离是速度曲线(平线)下方累积到时间t的面积。
为了说明原因,我们假设汽车行驶了一段时间,比如1/2个小时。在这种情况下,汽车行驶的距离为30英里,因为距离等于速度乘以时间,即60×1/2=30。重点在于,我们通过平线下方t=0和t=1/2小时之间的灰色矩形的面积,也能算出汽车行驶的距离(图7–2)。
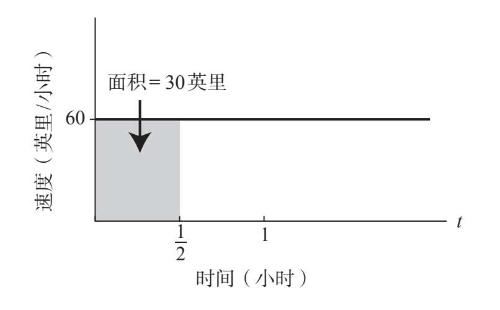
图7-2
用矩形的高(60英里/小时)乘以它的底(1/2小时),得出它的面积为30英里,这就是汽车行驶的距离。
同样的推理过程适用于任意时间t,这样一来,矩形的底就变为t,它的高仍然是60,它的面积是60t。事实上,这正是我们想求解的距离,即y=60t。
所以,至少在这个速度完全恒定且速度曲线是一条平线的例子中,根据速度推断出距离的关键在于计算速度曲线下方的面积。牛顿的见解是,即使速度不是恒定的,面积和距离之间的这个等式也会一直成立。不管物体的运动有多么不规律,它的速度曲线下方累积到时间t的面积总会等于它在t小时后行驶的距离。这是基本定理的版本之一,它似乎容易得让人难以置信,但事实的确如此。
牛顿之所以会产生这样的见解,是因为他把面积看作一个流动或移动的量,而不是按照当时几何学的惯例,把面积视为对形状的一种静态度量。他把时间引入几何学,并用物理学的眼光去看待它。如果牛顿现在还活着,他可能会把图7–2想象成动画,而且相较于快照,它更像翻页书。为了做到这一点,请再看一次图7–2,不过现在我们要把它想象成电影中的一帧或者翻页书中的一页。当动画在我们的脑海中播放时,我们会看到灰色矩形在做什么呢?它正在向一侧扩张。为什么呢?因为它的底(t)随时间的推移而增加。如果我们可以为每个时刻都制作一帧画面,并像翻动翻页书那样按顺序重新播放它们,动画版的灰色矩形看起来就在向右延伸。它类似于一个正在伸出的活塞,或者一支横放的注射器,正在将灰色液体吸入针筒。
灰色液体代表矩形不断扩大的面积,所以我们认为速度曲线v(t)下方的面积是“不断累积”的。在这个例子中,累积到时间t的面积是A(t)=60t,这与汽车行驶的距离y(t)=60t一致。因此,速度曲线下方的累积面积会给出距离随时间变化的情况。这是运动版的基本定理。