恒定的加速度
我们的最终目标是找到牛顿基本定理的通用几何版本,它是用抽象曲线y(x)及其下方的累积面积A(x)表示的。尽管累积面积的概念是解释这个定理的关键,但我意识到我们需要一些时间来适应这个概念,所以在用它来处理抽象的几何实例之前,我们先将它应用于一个更加具体的运动问题。
假设有一个以恒定加速度运动的物体,这意味着它的速度会越来越快,并且以恒定的速率增加,和汽车起步时踩油门的情况差不多。1秒钟后,汽车可能以10英里/小时的速度行驶;2秒钟后,速度变为20英里/小时;3秒钟后,速度变为30英里/小时,以此类推。在这个假设性的例子中,汽车的速度每过1秒就会增加10英里/小时,这个速度变化率被定义为汽车的加速度。(为简单起见,我们忽略了一个事实:一辆真实的汽车会有一个它无法超越的最高速度,当你踩下油门时,它的加速度可能也不是严格恒定的。)
在这个理想化的例子中,汽车每个时刻的速度都由线性函数v(t)=10t给出,其中数字10表示汽车的加速度。如果加速度是其他常数,比如a,那么这个公式可以泛化为:
v(t)=at
我们想知道,对这样一辆车来说,它从时间0至t行驶的距离是多少?换句话说,它从起点开始行驶的距离是如何随时间增加的?如果你使用中学学过的“距离等于速度乘以时间”的公式来解这道题,结果将会大错特错,因为这个公式只在速度恒定的情况下才有效,但这个例子中的速度并不是恒定的,而是每时每刻都在增加。我们已经告别了死气沉沉的匀速世界,来到了令人兴奋的加速度恒定的世界。
中世纪的学者[1]已经知道上述问题的答案了。牛津大学莫顿学院的哲学家和逻辑学家威廉·海特斯伯里早在1335年前后就解决了这个问题,法国的牧师和数学家尼科尔·奥雷斯姆在1350年前后进一步形象地分析了这个问题。遗憾的是,他们的成果没有得到广泛的研究,很快就被遗忘了。大约250年后,伽利略通过实验证明了恒定加速度并不是一种纯粹的学术假设。实际上,它是铁球之类的重物在地表附近自由下落或者滚下缓坡时的运动方式。在这两种情况下,球的速度v确实与时间t成正比,即v=at,这与加速度恒定的运动过程一样。
接下来,已知速度按照v=at呈线性增长,那么距离会如何增长呢?基本定理认为,行驶的距离等于速度曲线下方累积到时间t的面积。而且,这里的速度曲线是斜线v=at,所以相关的面积很容易计算,它等于图7–3中灰色三角形的面积。
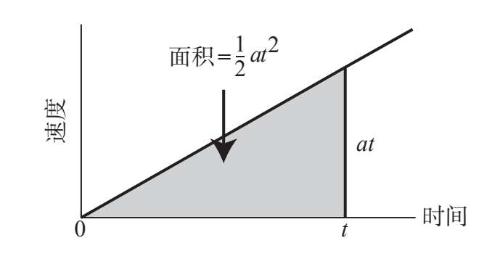
图7-3
和前一个问题中的灰色矩形一样,这里的灰色三角形的面积也会随着时间的推移而扩大。不同之处在于,矩形只在水平方向上延伸,而三角形则在两个方向上延伸。为了计算灰色三角形面积扩大的速度,我们观察到在任意时刻t它的底都是t,而它的高是物体当前的速度,即v=at。由于三角形的面积是底与高乘积的1/2,因此累积面积等于1/2×t×at=(1/2)at2。根据基本定理,速度曲线下方的面积就是物体运动的距离,即
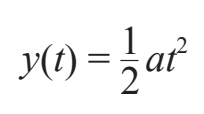
因此,对一个从静止状态开始均匀加速的物体来说,它运动的距离与所花费时间的平方成正比。这正是我们在第3章看到的伽利略的实验发现,他还用迷人的奇数定律将其表达出来。中世纪的学者也知道这一点。
但在中世纪甚至是伽利略生活的时代,人们还不知道当加速度不恒定时,速度会如何变化。换句话说,假设有一个以任意加速度a(t)运动的物体,它的速度v(t)会如何变化呢?
就像我在上一章提及的反向问题一样,这个问题也十分棘手。想要正确地理解它,关键是弄清楚已知和未知信息。
加速度的定义是速度的变化率。所以,如果速度函数v(t)已知,就很容易找到相应的加速度a(t),这被称作“解决正向问题”。就像我们运用放大抛物线的方法来计算它的斜率一样,我们可以通过计算速度函数的变化率来解决这个问题。而求解已知函数的变化率只需要利用导数的定义,以及不同函数的多种求导法则。
但反向问题的棘手之处在于,速度函数是未知的。假设速度函数的变化率(它的加速度)已知,我们要尝试计算什么样的速度函数才能满足这个变化率。如何从已知的变化率反向推导出未知的速度函数呢?这就像一个儿童游戏:“我想的是一个速度函数,它的变化率是这样那样的,那么我想的速度函数是什么呢?”
当我们试图依据速度推导距离时,也会出现需要进行反向推理的谜题。就像加速度是速度的变化率一样,速度是距离的变化率。正向推理很容易,如果我们知道一个运动物体行进的距离是时间的函数,就不难算出物体的瞬时速度,我们在上一章也做过这样的计算(博尔特参加北京奥运会短跑比赛的例子)。反向推理则很难,如果我告诉你博尔特在比赛中的瞬时速度,你能据此推导出每个时刻他在赛道上的位置吗?一般而言,已知任意一个速度函数v(t),你能推导出相应的距离函数y(t)吗?
牛顿的微积分基本定理为这类非常棘手的反向问题——从已知的变化率推断出未知的函数——提供了一种解决方案,并且在许多情况下都能将其彻底解决。其中的关键在于,把这类问题重构为一个关于可流动的和不断扩大的面积问题。
[1] Scholars in the Middle Ages: Katz, History of Mathematics, section 8.4.