用油漆滚筒证明基本定理
微积分基本定理是18世纪数学思想的巅峰。它通过动态的方式回答了一个静态的几何问题,从公元前250年古希腊的阿基米德、250年中国的刘徽、1000年开罗的海什木到1600年布拉格的开普勒,可能都问过这个问题。
我们来看一下图7–4中灰色区域的形状。
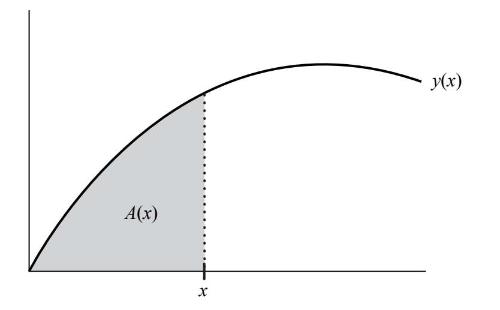
图7-4
假设该形状的顶部曲线可以是几乎所有形状,那么有没有一种方法能算出像它这样的任意形状的确切面积呢?尤其要注意,它不必是经典曲线,它有可能是某个方程在xy平面上定义的一条新奇的曲线。或者,如果这条曲线是由物理学感兴趣的事物来定义的,比如一个粒子的运动轨迹或者一道光线的传播路径,那么我们是否有办法系统地算出它下方的面积呢?这就是面积问题,也是我在前文中提到的微积分的第三个核心问题,还是17世纪中期最紧迫的数学挑战和曲线之谜中的最后一个未解难题。牛顿利用在运动和变化之谜中获得的启发,从一个新的方向走近这个问题。
从历史上看,解决这类问题的唯一方法就是头脑够聪明。你必须找到某种巧妙的方法把一个曲边区域切分成条块,或者把它打成碎片,然后在你的脑海中重新组合这些条块或碎片,或者像阿基米德那样在假想的跷跷板上称出它们的重量。但在1665年前后,牛顿给这个面积问题带来了近2 000年里从未有过的重大进展。尽管他吸收了伊斯兰代数和法国解析几何的见解,但却远远超越了它们。
根据牛顿的新体系,第一步是将这个面积放在xy平面上,并确定其顶部曲线的方程。这需要计算曲线在x轴上方的高度,也就是每次取一个垂直切片(如图7–4中虚线所示)以获得相应的y。这个计算过程可以把曲线转换成一个将y和x联系在一起的方程,以便用代数工具进行处理。早在30年前(17世纪40年代),费马和笛卡儿就充分了解了这一点,并运用这些技巧找到了曲线的切线,这本身就是一个巨大的突破。
但他们忽略了一点,那就是切线本身并没有那么重要。比切线更重要的是它们的斜率,因为正是斜率引出了导数的概念。就像我们在上一章看到的那样,作为曲线斜率的导数非常自然地出现在几何学中。在物理学中,导数也是作为其他变化率出现的,比如速度。因此,导数表明了斜率与速度之间的联系,更广泛地讲,是几何学和运动之间的联系。一旦导数的概念深深地扎根在牛顿的头脑中,它桥接几何学和运动的能力就会使最后的突破成为可能。而且,最终解决面积问题的正是导数。
当牛顿动态地看待面积问题时,所有这些概念——斜率与面积、曲线与函数、速率与导数——之间深藏的联系就从阴影中显现出来。秉持着我们在前两节内容中的研究精神,请你观察图7–4,并想象x以恒定的速度向右滑动。你甚至可以把x看作时间,牛顿经常这样做。然后,随着x的移动,灰色区域的面积会不断变化。这个面积取决于x,它应该被视为x的函数,所以我们把它写作A(x)。当我们想强调这个面积是x的函数(而不是一个固定的数)时,我们就称它为面积累积函数,有时简称为面积函数。
对于这个流动的场景(滑动的x和变化的面积),我高中的微积分老师乔夫雷先生打了一个令人难忘的比方。他让我们想象有一个神奇的油漆滚筒,当它平稳地向右滚动时,就会将曲线下方的区域涂成灰色(图7–5)。
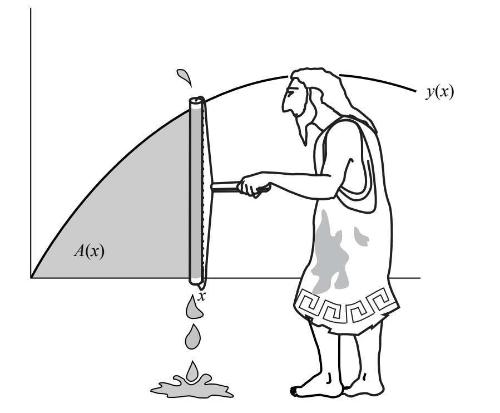
图7-5
x处的虚线表示这个假想的油漆滚筒当前的位置。同时,为了确保这个区域被恰当地刷好,滚筒会在垂直方向上魔法般地即时收缩或拉伸,正好触达顶部的曲线和底部的x轴,而不会越界。这个滚筒的神奇之处在于,它在滚动的过程中总能根据y(x)调整自己的长度,从而干净利落地刷好整个区域。
在设定了这个令人难以置信的场景之后,我们要解决的问题是:当x向右移动时,灰色区域的扩张速率是多少?或者说,当滚筒到达x处时,它刷油漆的速率是多少?为了回答这个问题,想想在下一个无穷小的时间间隔内会发生什么。答案是:滚筒会向右移动无穷小的距离dx。而且,当它滚过这个微小的距离时,它在垂直方向上的长度y几乎保持不变,因为在这个无限短的滚动过程中它几乎没有时间改变自己的长度(具体细节我们将在下一章再做讨论)。在这个短暂的时间间隔内,滚筒刷出来的是一个长而细的矩形:高为y,底为无穷小的dx,面积为无穷小的dA=ydx。将方程两边同时除以dx,就可以得到面积累积的速率:
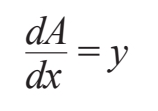
这个整洁的公式表明,曲线下方涂刷的总面积会以油漆滚筒当前的长度y的速率增大。这是有道理的:滚筒当前的长度越长,它在下一个瞬间刷的油漆就越多,面积累积的速率也越快。
只要稍加努力,我们就可以证明这个定理的几何版等价于我们之前用过的运动版,即速度曲线下方的累积面积等于运动物体行进的距离。但是,还有更急迫的任务在等着我们。我们需要理解这个定理意味着什么,它为什么重要,以及它最终是如何改变世界的。