自然的逻辑

自然的逻辑

微分方程的早期成就改变了西方文化的进程。1687年，牛顿构建了一个全新的世界体系[1]，展示了理性的力量并引发了启蒙运动[2]。他发现了一个小的方程组（他的运动和引力定律），它们可以解释伽利略、开普勒在地球上的落体和太阳系的行星轨道中发现的神秘规律。这样一来，他就消除了地球与其他天体之间的区别。在牛顿之后，只存在一个宇宙，同样的定律总是适用于所有地方。

在他的三卷本权威著作《自然哲学的数学原理》（通常简称为《原理》）中，牛顿将他的理论应用于更多地方：地球的形状（自转的离心力导致它的腰部略微隆起），潮汐的节律，彗星的偏心轨道，以及月亮的运动（这是一个非常难的问题，以至于牛顿向他的朋友埃德蒙·哈雷抱怨道，它“令我头痛，[3]常常让我夜不能寐，我不会再去想它了”）。

今天，大学生在学习物理学时，他们会先接触经典力学（牛顿力学），然后了解到它已经被爱因斯坦的相对论及普朗克、爱因斯坦、玻尔、薛定谔、海森伯和狄拉克的量子理论取代了。当然，这在很大程度上是真的。新理论推翻了关于空间与时间、质量与能量以及决定论本身的牛顿式概念，就量子理论而言，它对自然的描述更具概率论和统计学的特征。

但是，微积分所起的作用并未改变。和在量子力学中一样，自然律在相对论中仍然以微积分的语言写就，并以微分方程的形式表述。对我来说，这是牛顿最伟大的遗产，他证明了自然是合乎逻辑的。自然界中的因果关系和几何学中的证明一样，都是利用逻辑推理的方式由一个真理得出另一个真理，只不过前者是世界上的一个事件引发另一个事件，后者则是我们头脑中的一个想法产生另一个想法。

自然与数学之间的这种神秘联系可回溯至毕达哥拉斯的梦想。毕达哥拉斯学派发现了音乐和谐性与数之间的联系，并由此宣称“万物皆数”。对宇宙的运行而言，数很重要，形状也很重要，在伽利略梦寐以求的自然之书中，字词就是几何图形。尽管数和形状可能同等重要，但它们并不是这出戏剧的真正驱动者。在宇宙大戏中，数和形状好像演员，它们被一种看不见的存在——微分方程的逻辑——默默操控着。

牛顿是利用这个宇宙逻辑并围绕它建立体系的第一人。在他之前这是不可能做到的，因为必要的概念还未诞生。阿基米德对微分方程一无所知，伽利略、开普勒、笛卡儿和费马也不了解它。莱布尼茨虽然知道微分方程，但他的理解却不如牛顿那般科学，对数学的精通程度也比不上牛顿。所以，宇宙的神秘逻辑只被赐予了牛顿一人。

他的理论核心就是他的运动微分方程：

F=ma

这是历史上最重要的方程之一。它描述的是，作用于一个运动物体的力F等于该物体的质量m与它的加速度a的乘积。它之所以是一个微分方程，是因为加速度是一个导数（物体速度的变化率），或者用莱布尼茨的话说，它是两个微分之比：

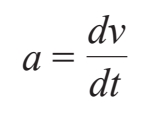
在这里，dv表示物体的速度v在无穷小的时间间隔dt内的无穷小的变化量。所以，如果已知作用于物体的力F和它的质量m，我们就可以利用方程F=ma并通过a=F/m算出它的加速度。加速度决定了物体的运动方式，它可以告诉我们物体的速度在下一个瞬间将会如何变化，物体的速度又可以告诉我们物体的位置将会如何变化。就这样，F=ma成了先知，它能预测物体未来的行为。

思考一下你能想到的最简单也是最荒凉的情景：一个孤立的物体独处于一个空空如也的宇宙中。它会如何移动呢？好吧，由于周围没有东西推动或者拉动它，作用于该物体的力F=0。又由于m不为0（假设物体是有质量的），根据牛顿定律可得F/m=a=0，这意味着dv/dt也等于0。但是，dv/dt=0意味着在无穷小的时间间隔dt内，这个孤立物体的速度没有改变，在下一个或之后的时间间隔内也不会改变。最终的结果是，当F=0时物体的速度永远保持不变。这就是伽利略的惯性定律：在没有外力作用的情况下，静止的物体会一直保持静止状态，运动的物体则会一直保持运动状态，而且速度和方向永远不会改变。我们刚刚推导出的惯性定律，就是牛顿运动定律F=ma的更深层次的逻辑结论。

早在上大学期间，牛顿似乎就知道了加速度与力成正比。他从伽利略的研究中了解到，如果一个物体没有受到外力作用，它要么保持静止，要么继续做匀速直线运动。他由此意识到，力并不是产生运动的必要条件，而是在运动中产生变化的必要条件，正是力使得物体加速、减速或者偏离直线路径。

比起更早的亚里士多德思想，这个见解是一个重大的进步。亚里士多德并不理解惯性，他认为只有力才能让物体保持运动。公平地说，在由摩擦力支配的情况下确实如此。如果你试图让桌子在地板上滑动，你就必须一直推它；一旦你不推了，桌子就会停止移动。但对划过太空的行星或者掉到地上的苹果来说，摩擦力的影响要小得多。在这些情况下，摩擦力微乎其微，在不遗失现象本质的情况下它可以忽略不计。

在牛顿的宇宙图景中，占支配地位的力是引力，而不是摩擦力。考虑到牛顿和引力在大众心目中的密切联系，这似乎是理所当然的。绝大多数人在想到牛顿时，都会立刻记起他们儿时学过的知识，即牛顿是在被苹果砸到头的时候[4]发现引力的。剧透警告：事实并非如此。发现引力的人不是牛顿，人们早已知道重物会下落。但没人知道引力的作用范围有多大，它的尽头是天空吗？

牛顿预感到引力可能会延伸到月球或更远的地方。他认为月球的运行轨迹是一个永不停歇地向着地球下落的过程，但与下落的苹果不同，下落的月球不会掉到地上，因为它同时也在惯性的作用下进行着侧向运动。就像伽利略从塔顶上扔下的铁球那样，月球在下落的同时向侧面滑动，形成一条弯曲的路径，只不过它向侧面滑动的速度很快，以至于月球永远无法到达在它的下方沿曲线轨道运行的地球表面。随着月球的轨道偏离直线，它开始加速（这并不是说它的速度改变了，而是它的运动方向改变了）。拉动它偏离直线路径的是地球引力持续不断的拖拽，由此产生的加速度被称为向心加速度，它倾向于将物体拉向中心（在这个例子中是地心）。

牛顿从开普勒第三定律推断出，引力随着距离的增大而减弱，这解释了为什么越遥远的行星绕太阳旋转一周的时间越长。他的计算表明，如果太阳拉动行星的力与让苹果落到地上及让月球保持轨道运动的力是同一种，这个力的大小就会与距离的平方成反比。因此，如果地球和月球之间的距离能以某种方式加倍，它们之间的引力就会减弱为原来的1/4（1/2的平方），而不是1/2。如果它们之间的距离变为原来的3倍，引力就会减弱为原来的1/9，而不是1/3。不可否认的是，牛顿的计算中包含一些可疑的假设，尤其是引力在相距遥远的情况下也能即时起作用（超距作用与即时性）的假设，就像浩瀚的太空无关紧要一样。尽管他不知道这是如何做到的，但平方反比定律仍然让他着迷不已。

为了对它进行定量检验，他根据已知的月球到地球的距离（约为地球半径的60倍）和已知的月球公转周期（约27天），估算出月球绕地球旋转的向心加速度。然后，他对月球的加速度与伽利略通过斜面实验测得的地球上落体的加速度进行了比较。牛顿发现这两个加速度相差一个因子，而且令人兴奋的是，这个因子接近3 600，即60的平方。这正是他的平方反比定律的预测结果：月球到地心的距离大约是苹果从树上掉到地上距离的60倍，因此月球的加速度应该是苹果加速度的1/3 600左右。后来牛顿回忆说，他“比较过使月球保持轨道运动[5]所需的力与地球表面的引力，并发现两者非常接近”。

那时，认为引力的拉动作用可能会延伸到月球的想法是疯狂的。还记得在亚里士多德学说中，月亮之下的一切都被视为易腐朽和不完美的，而在月亮照不到的地方，一切则是完美、不朽和永恒的。牛顿打破了这种范式，他把天和地统一起来，并且证明描述它们的物理学定律是一样的。

在发现平方反比定律的大约20年后，牛顿从对炼金术和圣经年代学的兴趣中暂时抽身出来，重新审视引力作用下的运动问题。他遭到了来自伦敦皇家学会的同事和竞争对手的挑衅，他们要求牛顿解决一个比他以前考虑过的问题难得多，而且他们也不知道如何解决的问题：如果来自太阳的吸引力按照平方反比定律减弱，那么行星会如何运动呢？据说，当他的朋友埃德蒙·哈雷提出这个问题时，牛顿立刻回答说“沿椭圆轨道运动”[6]。“但是，”大吃一惊的哈雷问道，“你是怎么知道的？”“因为我已经算过了。”牛顿说。当哈雷催促他解释推理过程时，牛顿开始重建他以前的相关研究。活力猛烈迸发，创造力也几乎和他在黑死病肆虐期间同样旺盛，就是在这样的状态下牛顿写作了《原理》一书。

通过将他的运动和引力定律假设成公理，并以微积分作为演绎工具，牛顿证明了开普勒的三大定律都符合逻辑必然性[7]。伽利略的惯性定律、单摆的等时性、球滚下斜坡的奇数规则和抛体的抛物线拱也一样，它们都是平方反比定律和F=ma的推论。这种诉诸演绎推理的做法让牛顿的同事大为震惊，也在哲学基础上撼动了他们。他们中的许多人都是经验主义者，认为逻辑只适用于数学本身，而自然必须通过实验和观察来研究。“自然拥有数学内核，自然现象可以从引力和运动定律等经验性公理通过逻辑推导得出”，牛顿的这些想法让他们目瞪口呆。