第10章 波、微波炉和脑成像
在19世纪初之前,热量一直是个谜。它到底是什么呢?它是像水一样的液体吗?它看起来确实在流动,但你却不能把它握在手里或者看见它。尽管你可以通过跟踪某个高温物体冷却过程中的温度变化来间接测量它,却没人知道在该物体内部发生了什么。
热量的秘密是由一个经常感到寒冷的人揭开的。傅里叶[1]10岁时就成了孤儿,十几岁时体弱多病,患有消化不良和哮喘。成年之后,他认为热量对健康来说至关重要。即使在夏天,他也会待在过热的房间里,并裹上一件厚大衣。在他的科学生涯的各个方面,傅里叶都专注和痴迷于热。他发明了全球变暖的概念,也是第一个解释温室效应会如何调节地球平均温度的人。
1807年,傅里叶利用微积分解开了热流[2]之谜。他提出了一个偏微分方程,可用于预测物体(比如一根炽热的铁棒)在冷却过程中温度的变化情况。傅里叶吃惊地发现,无论冷却过程开始时铁棒各处的温度有多么不均匀,这个偏微分方程都能轻松搞定。
想象一下,有一根又长又细的圆柱形铁棒在铁匠的锻炉里被不均匀地加热,它的周身散布着一些热点和冷点。为简单起见,我们假设铁棒外面有一个完全隔热的套筒,这样热量就不会散失了。在这种情况下,热流动的唯一途径是沿着铁棒的长度方向从热点扩散到冷点。傅里叶假定(并通过实验证实),铁棒上某一点的温度变化率正比于该点的温度与其两侧相邻点的平均温度之间的失配。我所说的相邻点是指,位于我们关注的那一点两侧的无限接近的两个点。
在这些理想化的条件下,热流的物理过程变得简单了。如果一个点比其相邻点冷,它就会升温;如果一个点比其相邻点热,它就会降温。失配越大,温度平衡的速度就越快。如果一个点的温度恰好等于其相邻点的平均温度,一切就平衡了,热量不再流动,这个点的温度在下一个瞬间也会保持不变。
通过比较一个点的瞬时温度与其相邻点的瞬时温度,傅里叶建立了一个偏微分方程,即我们现在所说的热传导方程。它包含两个自变量的导数:一个是时间(t)的无穷小变化量,另一个是铁棒上位置(x)的无穷小变化量。
傅里叶为自己设置的这个问题的难点在于,热点和冷点的初始排布有可能是杂乱无章的。为了解决这个一般性问题,傅里叶提出了一个看上去过度乐观,甚至有些鲁莽的方案。他声称可以用一个等效的简单正弦波之和来代替任意一种初始温度分布模式。
正弦波是他的构建单元,他之所以选择正弦波,是因为它们能使问题变得更加简单。他知道,如果温度分布一开始是正弦波模式,那么随着铁棒的冷却,它仍会保持这种模式(图10–1)。
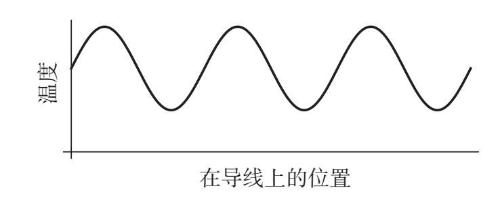
图10-1
关键在于,正弦波不会四处移动,它们就待在那里。的确,当它们的热点降温而冷点升温时,正弦波会减弱。但这种衰减很容易处理,它仅表示随着时间的推移温度变化趋于平缓。如图10–2所示,初始温度分布模式(虚线正弦波)会逐渐减弱,看起来就像实线正弦波一样。
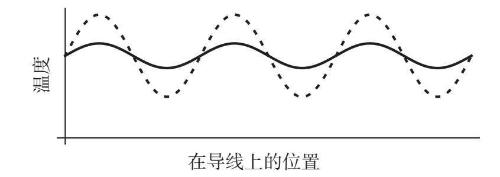
图10-2
重要的是,当正弦波减弱时,它们是静止不动的。也就是说,它们是驻波。
如果傅里叶能找到将原始温度模式分解成正弦波的方法,他就能分别解决每个正弦波的热流问题。他已经知道问题的答案了:每个正弦波都会发生指数式衰减,其衰减速度取决于它有多少个波峰和波谷。波峰越多的正弦波衰减得越快,因为它们的热点和冷点更紧致地挤在一起,这使得它们之间的热交换更迅速,从而更快地达到热平衡。在了解了每个正弦波的衰减情况后,傅里叶要做的就是把它们重新组合起来,去解决原始问题。
这一切的难点在于,傅里叶不经意间调用了正弦波的无穷级数。他又一次把无穷这个“石巨人”召唤到微积分中,而且傅里叶的做法比他的前辈更加不顾一切。他没有使用三角形碎片或三角形数的无穷级数和,而是漫不经心地采用了波的无穷级数和。这不禁让人联想到牛顿对幂函数xn的无穷级数和的处理方式,只不过牛顿从未声称他可以描述包括不连续跳跃或急转弯等可怕特征的任意复杂的曲线。而傅里叶偏偏宣称,包含转弯和跳跃的曲线并不能吓倒他。此外,傅里叶的正弦波是从微分方程本身自然产生的,从某种意义上说,它们是微分方程的固有振动模态或固有驻波模式,是为热流量身打造的。牛顿并未将幂函数当作构建单元,而傅里叶将正弦波视作构建单元,认为它们与热流问题有机地匹配在一起。
尽管傅里叶大胆使用正弦波作为构建单元的做法引发了争议,并且带来了棘手的严密性问题(数学家花了一个世纪的时间才解决它),但在我们的时代,傅里叶的伟大思想在计算机语音合成器和用于医疗成像的MRI扫描等技术中都发挥了重要作用。
[1] Fourier: Körner, Fourier Analysis, and Kline, Mathematics in Western Culture, chapter 19.For his life and work, see Dirk J.Struik, “Joseph Fourier,” Encyclopedia Britannica, https://www.britannica.com/biography/Joseph-Baron-Fourier.See also Grattan-Guinness, From the Calculus; Stewart, In Pursuit of the Unknown; Higham et al., The Princeton Companion; and Goriely, Applied Mathematics.
[2] heat flow: The mathematics of Fourier’s heat equation is discussed in Farlow, Partial Differential Equations, Katz, History of Mathematics, and Haberman, Applied Partial Differential Equations.