弦理论
正弦波也出现在音乐中,它们是吉他、小提琴和钢琴琴弦的固有振动模态。通过将牛顿力学和莱布尼茨的微积分应用于一根绷紧的弦的理想模型,我们可以推导出这种振动的偏微分方程。在这个模型中,弦被视为无穷小粒子的连续阵列,这些粒子并肩码放,相邻粒子通过弹力连接在一起。在任意时刻t,弦内的每个粒子都会根据它受到的力做相应的运动,这些力是在相邻粒子彼此拉拽的过程中由弦的张力产生的。在这些力已知的前提条件下,每个粒子都会根据牛顿定律F=ma做运动,而且这个过程发生在弦的每一点x上。由此建立的微分方程同时取决于x和t,它是偏微分方程的又一个例子。该方程被称为波动方程[1],果不其然,它预测出振动弦的典型运动是波。
就像在热流问题中一样,某些正弦波被证明有效,这是因为它们在振动时能自我再生。如果弦的两端被固定住,这些正弦波就无法传播,而只是待在原地进行振动。如果一根理想的弦受到的空气阻力和内摩擦力可以忽略不计,并且以正弦波模式开始振动,那么它将一直这样振动下去,振动频率也永远不会改变(图10–3)。出于所有这些原因,正弦波是解决这个问题的理想构建单元。
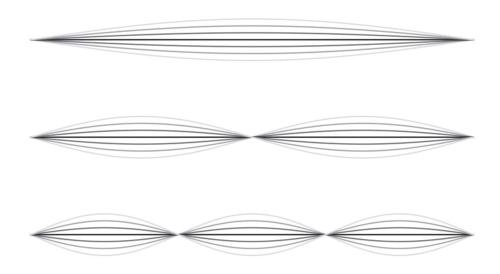
图10-3
其他振型同样可以由无穷多个正弦波加总而成。比如,在18世纪使用的羽管键琴中,一根弦在被松开前,往往会被用作琴拨的羽毛管拉成一个三角形(图10–4)。
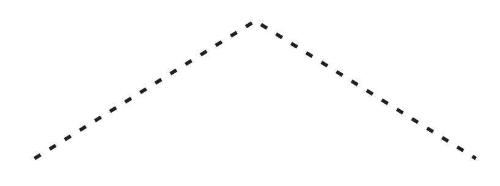
图10-4
尽管三角波有一个尖角,但它也可以表示成完全光滑的正弦波的无穷级数和形式。换句话说,我们不用尖角也能制造出尖角。在图10–5中,我通过3次越来越如实的逼近,用正弦波构建出一个近似三角波,如图中最下面的虚线所示。
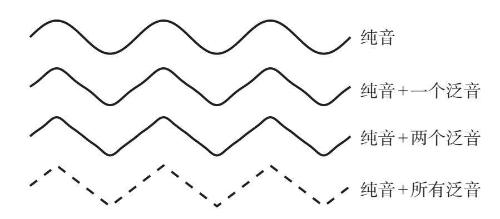
图10-5
第一次逼近的结果是一个具有最优可能振幅的正弦波(“最优”的意思是,它能让三角波的总平方误差最小化)。第二次逼近的结果是两个正弦波的最优和。第三次逼近的结果是三个正弦波的最优和。最优正弦波的振幅遵循傅里叶发现的一个公式:
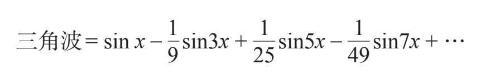
这个无穷级数和被称为三角波的傅里叶级数。请注意其中独特的数值模式:在正弦波中只出现了奇数频率,比如1, 3, 5, 7…,而且它们对应的振幅是正负号交替的奇数平方的倒数。遗憾的是,我无法用三言两语解释清楚这个公式为何有效;我们必须刻苦研究很多具体的微积分,才能弄明白公式中的那些神奇的振幅从何而来。但关键在于,傅里叶知道如何把它们计算出来。有了这个公式,他就能用简单得多的正弦波合成三角波或者其他任意复杂的曲线。
傅里叶的伟大思想是音乐合成器的基础,我们以一个音符(比如中央C上方的A)为例说明其中的原因。为了发出准确的音高,我们可以敲击一个振动频率被设定为440个周期/秒的音叉。音叉由一个把手和两个金属叉组成,当用橡胶锤敲击音叉时,金属叉每秒钟会来回振动440次。金属叉的振动会扰动附近的空气:向外振动时,它们会压缩空气;而向内振动时,它们会使周围的空气变得稀薄。空气分子的来回晃动又会产生正弦压力扰动,我们的耳朵将其当作一个纯音——单调沉闷的A音,它缺乏音乐家所说的音色。然而,我们可以用小提琴或钢琴弹奏出同样的A音,它听起来却生动又温暖。尽管小提琴或钢琴也在以440个周期/秒的基本频率振动,但由于搭配了不同的泛音,它们发出的声音与音叉(及其他乐器)不同。泛音就是三角波公式中像sin3x和sin5x这样的波对应的音乐术语,它通过加入多倍的基本频率为音符增色。除了频率为440个周期/秒的正弦波外,合成三角波中还包括一个正弦波泛音,它的频率是正弦波的3倍(3×440=1 320个周期/秒)。这个泛音不像基本的sinx模态那么强,它的相对振幅只是基本模态的1/9,其他奇数模态则更弱。从音乐角度说,振幅决定了泛音的响度,小提琴声音的丰富度与它的柔和泛音和响亮泛音的特定组合方式有关。
傅里叶思想的统一力量在于,任何乐器的声音都可以用无穷多个音叉合成。我们要做的只是在恰当的时间用恰当的力度去敲击音叉,尽管我们只用了单调沉闷的正弦波,却不可思议地演奏出小提琴、钢琴乃至小号或双簧管的声音。这就是第一批电子合成器的基本工作原理:通过组合大量的正弦波,它们可以再现任何乐器的声音。
高中时期我上过一节电子音乐课,从中感受到了正弦波的作用。那是在滞胀的20世纪70年代,当时的电子音乐是在一个看似老式交换机的大盒子产生的。我的同学和我先把电缆插入各种插口,再来回转动旋钮,就会听到正弦波、方波和三角波的声音。我还记得,正弦波的声音干净而宽广,就像长笛一样;方波的声音听起来尖利刺耳,就像火警警报一样;三角波的声音听起来则喧闹嘈杂。转动其中一个旋钮,我们可以改变波的频率,升降它的音高。转动另一个旋钮,我们可以改变波的振幅,使它听起来更响亮或更柔和。同时插入几根电缆,我们可以把波及其泛音以不同的形式组合在一起,这是我们对抽象的傅里叶理论的感官体验。我们在示波器上看到波的形状的同时,也能听到它们的声音。如今你可以在互联网上尝试这一切,搜索“三角波的声音”之类的内容,就能找到交互式演示程序。它们会让你觉得自己仿佛回到了1974年,正坐在我的教室里享受着玩转波的乐趣。
更重要的是,在利用微积分预测粒子连续介质的运动和变化方式上,傅里叶迈出了第一步。除牛顿对离散粒子运动的研究之外,这是又一个巨大的进步。在接下来的几个世纪里,科学家继续用傅里叶的方法去预测其他连续介质的行为,比如波音787客机机翼的颤振、患者接受面部手术后的外貌、流经动脉的血流或者地震后大地发出的隆隆声。如今,这些技术在科学和工程学领域无处不在,它们被用来分析各种波现象,包括:热核爆炸产生的冲击波,通信的无线电波,在肠内促使营养物质吸收并推动废物朝着正确方向移动的消化波;大脑中与癫痫和帕金森震颤相关的病理性电波,公路上的交通拥挤波(就像令人恼火的幽灵堵塞现象一样,交通在没有明显原因的情况下整体减速)。傅里叶思想及其分支可以帮助我们从数学角度理解所有这些波现象,对它们做出解释和预测(有时要借助公式,有时则要通过大规模的计算机模拟),在某些情况下还可以控制或消除它们。
[1] wave equation: For the mathematics of vibrating strings, Fourier series, and the wave equation, see Farlow, Partial Differential Equations; Katz, History of Mathematics; Haberman, Applied Partial Differential Equations; Stillwell, Mathematics and Its History; Burton, History of Mathematics; Stewart, In Pursuit of the Unknown; and Higham et al., The Princeton Companion.