为什么是正弦波？

为什么是正弦波？

在结束关于正弦波的讨论并转向其二维和三维对应物之前，我们有必要阐明它们的特别之处。毕竟，其他类型的曲线也可以用作构建单元，有时它们的效果甚至比正弦波还要好。比如，为了捕捉指纹脊线之类的局部特征，子波得到了美国联邦调查局的认可。在地震分析、艺术品修复与鉴别、面部识别等领域，子波在诸多图像处理与信号处理任务中的表现常常优于正弦波。

为什么正弦波非常适合做波动方程、热传导方程和其他偏微分方程的解呢？因为正弦波的优点在于，它们可以与导数“相处得十分融洽”。具体来说，一个正弦波的导数是另一个正弦波，两者之间存在1/4个周期的位移。这是一个了不起的特性，而其他类型的波并不具备。通常，当我们求任意一条曲线的导数时，它会因为微分而变得扭曲，所以求导前后它的形状是不一样的。对大多数曲线来说，求导都是一种痛苦的经历，但对正弦波来说则不然。在求导之后，正弦波会抖落身上的灰尘，表现得泰然自若，和求导之前没什么两样。它遭受的唯一伤害（其实根本算不上伤害）是时间上的变化，即它会比求导之前提早1/4个周期达到峰值。

我们在第4章研究过一个不太完美的此类案例——2018年纽约市昼长的每天变化情况，并将其与昼长变化率的每天变化情况进行了比较。我们看到这两条曲线都近似于正弦曲线，只不过表示昼长变化率的正弦波比表示昼长的正弦波提早了3个月。简言之，2018年昼长最长的一天是6月21日，而昼长加长率最快的一天是3个月前的3月20日，这就是我们期望从正弦曲线中看到的情况。如果昼长数据是完美的正弦波，而且我们观察的不是每天的变化而是每个瞬间的变化，那么它的瞬时变化率（“导数”波）本身就是完美的正弦波，并且正好提早了1/4个周期。在第4章我们也看到了这1/4个周期的位移为何会发生，它源于正弦波与匀速圆周运动之间的深层联系。

1/4个周期的位移是一个十分有趣的结果。它表明，如果我们对正弦波求导两次，它就会提早1/4个周期再加上1/4个周期，所以它总共提早了1/2个周期。这意味着之前的波峰现在变成了波谷，反之亦然；正弦波完全颠倒了。在数学上，这个过程可以用下面的公式来表达：

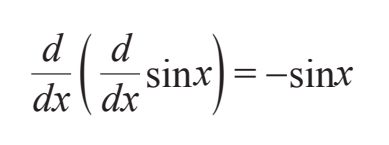
其中，莱布尼茨的微分符号d/dx表示“对右边的表达式求导”。这个公式表明，对sinx求导两次就相当于让它乘以–1。用一次简单的乘法运算代替两次求导，是一种神奇的简化方式。求导两次是十分烦琐的微积分运算，而乘以–1是中学水平的算术。

不过你可能想问，为什么有人要对某个东西求导两次呢？因为自然一直是这样做的，更确切地说，我们的自然模型一直是这样做的。比如，在牛顿的运动定律F=ma中，加速度a就涉及两次求导。想知道其中的原因，你需要记住加速度是速度的导数，而速度又是距离的导数。因此，加速度是距离的导数的导数，或者更简单地说，加速度是距离的二阶导数。二阶导数在物理学和工程学领域随处可见，除牛顿方程之外，它们还在热传导方程和波动方程中扮演着重要角色。

这就是正弦波非常适合于这些方程的原因。对正弦波来说，两次求导的结果仅相当于乘以–1。实际上，当我们只关注正弦波时，让热传导方程和波动方程变得难以分析的微积分就不再是问题了。微积分会被剔除并代之以乘法，这让与正弦波有关的振动弦问题和热流问题变得更容易解决。如果一条曲线可以由正弦波构成，那么它将继承正弦波的优点。唯一的困难在于，构建一条曲线需要将无穷多个正弦波叠加在一起，但这不过是一个小小的代价。

这就是从微积分的角度看正弦波之所以特别的原因。物理学家也有他们自己的观点，同样值得我们了解。对物理学家来说，正弦波（在振动和热流问题的语境中）的非凡之处在于，它们会形成驻波。驻波不会沿着弦或铁棒移动，而会待在原地；尽管它们会上下振动，但从不传播。更引人注目的是，驻波会以单一频率振动，这在波的世界里非常少见。大多数波都是诸多频率的组合，比如，白光是由彩虹的所有颜色的光混合而成的。从这个方面看，驻波是纯粹的波，而不是混合波。